
【题目】菱形ABCD中,∠ABC=60°,BD=![]() ,点E在AB上,CE=
,点E在AB上,CE=![]() ,将CE绕点C旋转60°交线段BD于F,则DF的长为 _________________.
,将CE绕点C旋转60°交线段BD于F,则DF的长为 _________________.
【答案】![]()
【解析】连接AC,如图所示:

∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD=![]() BD=
BD=![]() ,AB=BC=CD=DA,
,AB=BC=CD=DA,
∵∠ABC=60°,
∴△ABC、△ACD是等边三角形,
∴AC=AB=CD=AD,∠ACB=∠CAD=∠ACD=60°,
∴AB= ,
,
∴CD=AB=6,
∵∠ECM=60°,
∴∠BCE=∠ACM,
在△BCE和△ACM中,
∠EBC=∠MAC=60°,BC=AC,∠BCE=∠ACM,
∴△BCE≌△ACM(ASA),
∴CE=CM=![]() ,
,
作MG⊥CD于G,设DG=x,则DM=2x,MG=![]() x,CG=6x,
x,CG=6x,
根据勾股定理得:CG2+MG2=CM2,
即(6x)2+(![]() x)2=(
x)2=(![]() )2,
)2,
解得:x=1或2,
∴2x=2或4,即DM=2或4.
∵![]()
∴![]()
∴![]()
即![]() 或
或![]()
∴![]() 或
或![]()
故答案为: ![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.
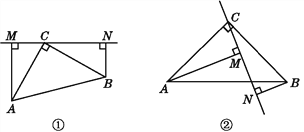
(1)试说明:MN=AM+BN.
(2)如图②,若过点C作直线MN与线段AB相交,AM⊥MN于点M,BN⊥MN于点N(AM>BN),(1)中的结论是否仍然成立?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com