
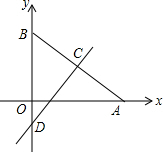
 如图,在平面直角坐标系中,点A在x轴的正半轴上,点B在y轴的正半轴上,且线段OA,OB(OB<OA)的长是方程x2-7x+12=0的两个根,过线段AB的中点C作CD⊥AB交y轴于点D.
如图,在平面直角坐标系中,点A在x轴的正半轴上,点B在y轴的正半轴上,且线段OA,OB(OB<OA)的长是方程x2-7x+12=0的两个根,过线段AB的中点C作CD⊥AB交y轴于点D.分析 (1)根据题意,求出方程x2-7x+12=0的两个根,即可求出OA,OB的长各是多少.
(2)首先求出A、B两点的坐标,进而求出线段AB的中点C的坐标;然后根据CD⊥AB,求出CD所在的直线的斜率;最后应用点斜式,求出直线DC的解析式即可.
(3)在坐标平面内存在点M,使以A,B,D,M为顶点的四边形是平行四边形.根据题意,分三种情况讨论:①点M在第四象限时;②点M在第二象限时;③点M在第一象限时;根据平行四边形的性质,求出点M的坐标各是多少即可.
解答 解:(1)由x2-7x+12=0,可得
x1=4,x2=3,
∵线段OA,OB(OB<OA)的长是方程x2-7x+12=0的两个根,
∴OA=4,OB=3.
(2)∵OA=4,点A在x轴的正半轴上,
∴点A的坐标是(4,0),
∵OB=3,点B在y轴的正半轴上,
∴点B的坐标是(0,3),
∴线段AB的中点C的坐标是(2,$\frac{3}{2}$),
∵AB所在的直线的斜率是:$\frac{3-0}{0-4}$=-$\frac{3}{4}$,且CD⊥AB,
∴CD所在的直线的斜率是$\frac{4}{3}$,
∴直线DC的解析式是:
y-$\frac{3}{2}$=$\frac{4}{3}$(x-2),
即直线DC的解析式是8x-6y-7=0.
(3)在坐标平面内存在点M,使以A,B,D,M为顶点的四边形是平行四边形.
∵直线DC的解析式是8x-6y-7=0,CD交y轴于点D,
∴点D的坐标是(0,-$\frac{7}{6}$).
①如图1,AD、BM交于点E,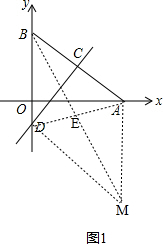 ,
,
∵AM∥BD,
∴点M的横坐标是4,不妨设点M的坐标是(4,b),
∵四边形ABDM是平行四边形,
∴点E既是AD,又是BM的中点,
∵点A的坐标是(4,0),点D的坐标是(0,-$\frac{7}{6}$),
∴点E的坐标是(2,-$\frac{7}{12}$),
又∵点E是BM的中点,
∴3+b=2×(-$\frac{7}{12}$)=-$\frac{7}{6}$,
解得b=-$\frac{25}{6}$,
∴点M的坐标是(4,-$\frac{25}{6}$).
②如图2,BD、AM交于点F,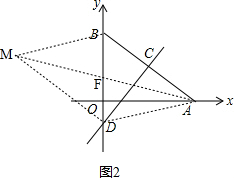 ,
,
∵四边形ABMD是平行四边形,
∴点F既是BD,又是AM的中点,
设点M的坐标是(a,b),
则$\left\{\begin{array}{l}{\frac{a+4}{2}=0}\\{\frac{b+0}{2}=\frac{3-\frac{7}{6}}{2}}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=-4}\\{b=\frac{11}{6}}\end{array}\right.$
∴点M的坐标是(-4,$\frac{11}{6}$).
③如图3,AB、DM交于点C,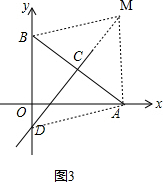 ,
,
∵四边形AMBD是平行四边形,
∴点C既是AB,又是DM的中点,
设点M的坐标是(c,d),
则$\left\{\begin{array}{l}{\frac{4+0}{2}=\frac{c+0}{2}}\\{\frac{0+3}{2}=\frac{d-\frac{7}{6}}{2}}\end{array}\right.$
解得$\left\{\begin{array}{l}{c=4}\\{d=\frac{25}{6}}\end{array}\right.$
∴点M的坐标是(4,$\frac{25}{6}$).
综上,可得
在坐标平面内存在点M,使以A,B,D,M为顶点的四边形是平行四边形,
点M的坐标是(4,-$\frac{25}{6}$),(-4,$\frac{11}{6}$)或(4,$\frac{25}{6}$).
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了平行四边形的性质和应用,要熟练掌握,解答此题的关键是要明确:平行四边形的性质:①边:平行四边形的对边相等.②角:平行四边形的对角相等.③对角线:平行四边形的对角线互相平分.
(3)此题还考查了直线的解析式的求法,要熟练掌握.


科目:初中数学 来源: 题型:解答题
| 平均数 | 中位数 | 方差 | 命中10环的次数 | |
| 甲 | 7 | 7 | 2.8 | 0 |
| 乙 | 7 | 7.5 | 5.4 | 1 |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,CE是⊙O的切线,且AE⊥CE,垂足为E,BC的延长线交AE的延长线于点D.
如图,AB为⊙O的直径,CE是⊙O的切线,且AE⊥CE,垂足为E,BC的延长线交AE的延长线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
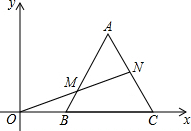 如图,在平面直角坐标系中,等边三角形ABC的顶点B、C的坐标分别为(2,0),(6,0),点N从A点出发沿AC向C点运动,连接ON交AB于点M.当边AB恰平分线段ON时,则AN=2.
如图,在平面直角坐标系中,等边三角形ABC的顶点B、C的坐标分别为(2,0),(6,0),点N从A点出发沿AC向C点运动,连接ON交AB于点M.当边AB恰平分线段ON时,则AN=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com