
【题目】如图,在RtΔABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BE ⊥AD交AC的延长线于F,E为垂足.则结论:(1)AD=BF;(2)CF=CD;(3)AC +CD=AB;(4)BE=CF;(5)BF=2BE,其中正确的结论个数是( ).

A. 2 B. 3 C. 4 D. 5
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】某花卉种植基地欲购进甲、乙两种君子兰进行培育。若购进甲种2株,乙种3株,则共需成本l700元;若购进甲种3株,乙种l株.则共需成本l500元。
(1)求甲、乙两种君子兰每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下购入甲、乙两种君子兰,若购入乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对当年初中升高中数学考试成绩进行抽样分析,试题满分100分,将所得成绩(均为整数)整理后,绘制了如图所示的统计图,根据图中所提供的信息,回答下列问题:

(1)共抽取了多少名学生的数学成绩进行分析?
(2)如果80分以上(包括80分)为优生,估计该年的优生率为多少?
(3)该年全市共有22000人参加初中升高中数学考试,请你估计及格(60分及60分以上)人数大约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长方形的周长是12cm,期中一条边为x cm(x>0),面积为y cm,则这个长方形的面积y与边长x的关系可以表示为( )
A.y=(6-x)xB.y=xC.y=x(12-x)D.y=2(6-x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料
通过小学的学习我们知道,分数可分为“真分数”和“假分数”.而假分数都可化为带分数,如: ![]() .
.
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
如: ![]() ,
, ![]() 这样的分式就是假分式;再如:
这样的分式就是假分式;再如: ![]() ,
, ![]() 这样的分式就是真分式.
这样的分式就是真分式.
类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).
如: ![]() ;
; ![]() ;
;
再如: ![]() .
.
解决下列问题:
(1)分式![]() 是 分式(填“真分式”或“假分式”);
是 分式(填“真分式”或“假分式”);
(2)假分式![]() 可化为带分式 的形式;
可化为带分式 的形式;
(3)如果分式![]() 的值为整数,那么x的整数值为 .
的值为整数,那么x的整数值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 三边的长分别为
三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.
,求这个三角形的面积.
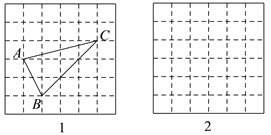
小明同学在解答这道题时,先建立了一个正方形网格(每个小正方形的边长为1),再在网格中
画出格点△ABC中,(即△ABC三个顶点都在小正方形的顶点处),如图1所示,这样不需要△ABC高,借用网格就能计算出它的面积.
(1)△ABC的面积为 ;
(2)如果△MNP三边的长分别为![]() ,
, ![]() ,
, ![]() ,请利用图2的正方形网格(每个小正方形的边长为1)画出相应的格点△MNP,并直接写出△MNP的面积为 .
,请利用图2的正方形网格(每个小正方形的边长为1)画出相应的格点△MNP,并直接写出△MNP的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )

A.内部 B.外部 C.边上 D.以上都有可能
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com