
 已知二次函数y=-9x2-6ax-a2+2a;
已知二次函数y=-9x2-6ax-a2+2a;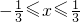 时有最大值-4,求a的值.
时有最大值-4,求a的值. ,且对称轴在y轴左侧,
,且对称轴在y轴左侧,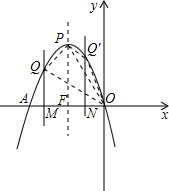 ②当
②当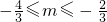 时,QM=-9m2-12m,OM=-m,OF=
时,QM=-9m2-12m,OM=-m,OF= ,PF=4,
,PF=4, ≤m<0时,QN=-9m2-12m,FN=
≤m<0时,QN=-9m2-12m,FN= +m,PF=4,
+m,PF=4, ,
,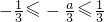 时,则-1≤a≤1,y最大=2a=-4,a=-2,不成立;
时,则-1≤a≤1,y最大=2a=-4,a=-2,不成立;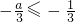 时,则a≥1,当
时,则a≥1,当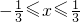 时,y随x的增大而减小,
时,y随x的增大而减小,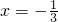 ,y最大=-a2+4a-1=-4,
,y最大=-a2+4a-1=-4,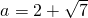 ,而
,而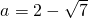 舍去;
舍去;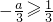 时,则a≤-1,当
时,则a≤-1,当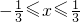 时,y随x的增大而增大,
时,y随x的增大而增大, ,y最大=-a2-1=-4,
,y最大=-a2-1=-4,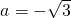 ,而
,而 舍去
舍去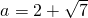 或
或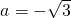
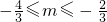 时,②当
时,②当 ≤m<0时,分别画出图形,可表示出S关于m的函数关系式.
≤m<0时,分别画出图形,可表示出S关于m的函数关系式.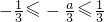 时,②当
时,②当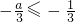 时,③当
时,③当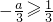 时,分别求出函数的最大值,再由二次函数在
时,分别求出函数的最大值,再由二次函数在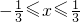 时有最大值-4,可作出取舍.
时有最大值-4,可作出取舍.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| A、y1≥y2 | B、y1>y2 | C、y1<y2 | D、y1≤y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:查看答案和解析>>
科目:初中数学 来源: 题型:
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com