
����Ŀ��(2016�㽭ʡ��ɽ�е�22��)��ͼ1����֪��E��F��G��H�ֱ����ı���ABCD����AB��BC��CD��DA���е㣬��������˼·����֤���ı���EFGH��ƽ���ı��Σ�
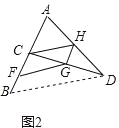
��1����ͼ2����ͼ1�еĵ�C�ƶ������E�غϵ�λ�ã�F��G��H����BC��CD��DA���е㣬��֤���ı���CFGH��ƽ���ı��Σ�
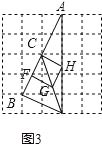
��2����ͼ3���ڱ߳�Ϊ1��С��������ɵ�5��5�����У���A��C��B���ڸ���ϣ��ڸ���ϻ�����D��ʹ��C��BC��CD��DA���е�F��G��H���������CFGH��
��3���ڣ�2�����������������CFGH�ı߳���
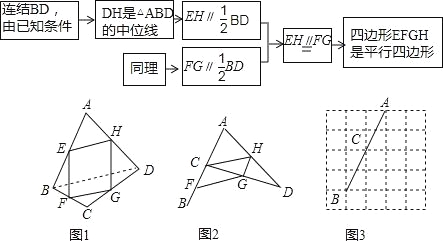
���𰸡�(1)��֤�����̼�������(2)��ͼ�μ�������(3)��![]()
��������
���������(1)������BD���������ε���λ�ߵ����ʵõ�CH��BD��CH=![]() BD��ͬ��FG��BD��FG=
BD��ͬ��FG��BD��FG=![]() BD����ƽ���ı��ε��ж��������ɵõ����ۣ�(2)�����������ε���λ�ߵ����ʺ������ε����ʼ��ɵõ������(3)�����ݹ��ɶ����õ�BD=
BD����ƽ���ı��ε��ж��������ɵõ����ۣ�(2)�����������ε���λ�ߵ����ʺ������ε����ʼ��ɵõ������(3)�����ݹ��ɶ����õ�BD=![]() ���������ε���λ�ߵ����ʵõ�FG=
���������ε���λ�ߵ����ʵõ�FG=![]() BD=
BD=![]() �����ǵõ����ۣ�
�����ǵõ����ۣ�
���������(1)����ͼ2������BD����C��H��AB��DA���е㣬 ��CH����ABD����λ�ߣ�
��CH��BD��CH=![]() BD�� ͬ��FG��BD��FG=
BD�� ͬ��FG��BD��FG=![]() BD�� ��CH��FG��CH=FG�� ���ı���CFGH��ƽ���ı��Σ�
BD�� ��CH��FG��CH=FG�� ���ı���CFGH��ƽ���ı��Σ�
(2)����ͼ3��ʾ��
(3)����ͼ3����BD=![]() ����FG=
����FG=![]() BD=
BD=![]() ����������CFGH�ı߳���
����������CFGH�ı߳���![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016�㽭ʡ��ɽ�е�9��)��ͼ������ABCD�У�AD=2��AB=3������A��C�����Ϊ2��ƽ���߶�AE��CF���ֱ�CD��AB�ڵ�E��F����DE�ij��ǣ� ��
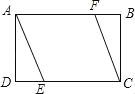
A��![]() B��
B��![]() C��1 D��
C��1 D��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԪ����x2+x��2��0��һ�����ǩ�2����÷��̵���һ�����ǣ�������
A. 1 B. ��1 C. 2 D. ��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ЦЦ��ƽ��ֱ������ϵ�л���һ�κ���y��kx+b��ͼ����һ�����������ޣ���k��ֵ�����ǣ� ��
A.4B.0C.��1D.��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
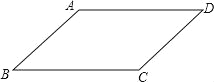
����Ŀ��(2016�㶫ʡï���е�18��)ijͬѧҪ֤��������ƽ���ı��εĶԱ���ȣ�������ȷ�ģ���������ͼ�Σ���д����������֪�Ͳ���������֤��
��֪����ͼ���ı���ABCD��ƽ���ı��Σ�
��֤��AB=CD��
��1����ȫ��֤���֣�
��2������д��֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016�㶫ʡ÷���е�22��)
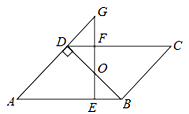
��ͼ��ƽ���ı���ABCD�У�BD��AD����A=45����E��F�ֱ���AB��CD�ϵĵ�����BE=DF������EF��BD��O��
��1����֤��BO=DO��
��2����EF��AB���ӳ�EF��AD���ӳ�����G����FG=1ʱ����AE�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com