
如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分
∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF?AC,cos∠ABD=![]() ,AD=12.
,AD=12.
⑴求证:△ANM≌△ENM;
⑵求证:FB是⊙O的切线;
⑶证明四边形AMEN是菱形,并求该菱形的面积S.

.⑴证明:∵BC是⊙O的直径
∴∠BAC=90o
又∵EM⊥BC,BM平分∠ABC,
∴AM=ME,∠AMN=EMN
又∵MN=MN,
∴△ANM≌△ENM
⑵∵AB2=AF?AC
∴![]()
又∵∠BAC=∠FAB=90o
∴△ABF∽△ACB
∴∠ABF=∠C
又∵∠FBC=∠ABC+∠FBA=90o
∴FB是⊙O的切线
⑶由⑴得AN=EN,AM=EM,∠AMN=EMN,
又∵AN∥ME,∴∠ANM=∠EMN,
∴∠AMN=∠ANM,∴AN=AM,
∴AM=ME=EN=AN
∴四边形AMEN是菱形
∵cos∠ABD=![]() ,∠ADB=90o
,∠ADB=90o
∴![]()
设BD=3x,则AB=5x,,由勾股定理![]()
而AD=12,∴x=3
∴BD=9,AB=15
∵MB平分∠AME,∴BE=AB=15
∴DE=BE-BD=6
∵ND∥ME,∴∠BND=∠BME,又∵∠NBD=∠MBE
∴△BND∽△BME,则![]()
设ME=x,则ND=12-x,![]() ,解得x=
,解得x=![]()
∴S=ME?DE=![]() ×6=45
×6=45


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
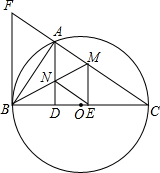 如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF•AC,cos∠ABD=
如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF•AC,cos∠ABD=| 3 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•浦口区一模)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=70°,BC=2,则图中阴影部分面积为
(2012•浦口区一模)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=70°,BC=2,则图中阴影部分面积为| 7 |
| 18 |
| 7 |
| 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:
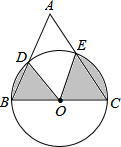 (2013•眉山)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为
(2013•眉山)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•攀枝花)如图,以BC为直径的⊙O1与⊙O2外切,⊙O1与⊙O2的外公切线交于点D,且∠ADC=60°,过B点的⊙O1的切线交其中一条外公切线于点A.若⊙O2的面积为π,则四边形ABCD的面积是
(2012•攀枝花)如图,以BC为直径的⊙O1与⊙O2外切,⊙O1与⊙O2的外公切线交于点D,且∠ADC=60°,过B点的⊙O1的切线交其中一条外公切线于点A.若⊙O2的面积为π,则四边形ABCD的面积是| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com