
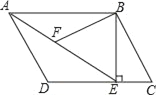
【题目】如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠BFE=∠C.
(1)求证:△ABF∽△EAD;
(2)若AB=4,∠BAE=30°,求AE的长.
科目:初中数学 来源: 题型:
【题目】某学校办公楼前有一长为![]() ,宽为
,宽为![]() 的长方形空地,在中心位置留出一个半径为
的长方形空地,在中心位置留出一个半径为![]() 的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.
的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.

(1)用含字母和![]() 的式子表示阴影部分的面积;
的式子表示阴影部分的面积;
(2)当![]() =4,
=4,![]() =3,
=3,![]() =1,
=1,![]() =2时,阴影部分面积是多少?(
=2时,阴影部分面积是多少?(![]() 取3)
取3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB的两端点的坐标为A(﹣1,0),B(0,﹣2).现请你在坐标轴上找一点P,使得以P、A、B为顶点的三角形是直角三角形,则满足条件的P点的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
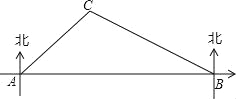
【题目】如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=400m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数![]() (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(1)求△OCD的面积;
(2)当BE=![]() AC时,求CE的长.
AC时,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
![]()
![]() 若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
![]() 若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
![]() 若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代的数学专著,是“算经十书”(汉唐之间出现的十部古算书)中最重要的一种.书中有下列问題:“今有邑方不知大小,各中开门,出北门八十步有木,出西门二百四十五步见木,问邑方有几何?”意思是:如图,点![]() 、点
、点![]() 分别是正方形
分别是正方形![]() 的边
的边![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() 过点
过点![]() ,
,![]() 步,
步,![]() 步,则正方形的边长为( )
步,则正方形的边长为( )

A.![]() 步B.
步B.![]() 步C.
步C.![]() 步D.
步D.![]() 步
步
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com