
【题目】《九章算术》是中国古代的数学专著,是“算经十书”(汉唐之间出现的十部古算书)中最重要的一种.书中有下列问題:“今有邑方不知大小,各中开门,出北门八十步有木,出西门二百四十五步见木,问邑方有几何?”意思是:如图,点![]() 、点
、点![]() 分别是正方形
分别是正方形![]() 的边
的边![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() 过点
过点![]() ,
,![]() 步,
步,![]() 步,则正方形的边长为( )
步,则正方形的边长为( )

A.![]() 步B.
步B.![]() 步C.
步C.![]() 步D.
步D.![]() 步
步
科目:初中数学 来源: 题型:
【题目】某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 | 管理人员 | 普通工作人员 | |||||
人员结构 | 总经理 | 部门经理 | 科研人员 | 销售人员 | 高级技工 | 中级技工 | 勤杂工 |
员工数(名) | 1 | 3 | 2 | 3 | 24 | 1 | |
每人月工资(元) | 21000 | 8400 | 2025 | 2200 | 1800 | 1600 | 950 |
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数x为2500元,中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员.请你回答右图中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资![]() (结果保留整数),并判断
(结果保留整数),并判断![]() 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
A.中位数就是一组数据中最中间的一个数
B.这组数据0,2,3,3,4,6的方差是2.1
C.一组数据的标准差越大,这组数据就越稳定
D.如果![]() 的平均数是
的平均数是![]() ,那么
,那么![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在①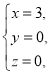 ②
②![]() ③
③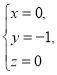 这三对数值中,__________是方程x+2y+z=3的解,__________是方程2x-y-z=1的解,__________是方程3x-y-z=2的解,因此__________是方程组
这三对数值中,__________是方程x+2y+z=3的解,__________是方程2x-y-z=1的解,__________是方程3x-y-z=2的解,因此__________是方程组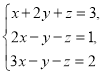 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学实践活动课上,老师拿出三个边长都为5cm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
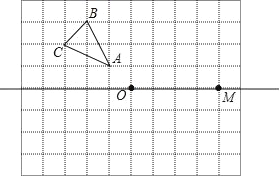
【题目】如图,它是一个8×10的网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.
(1)画出△ABC关于直线OM对称的△A1B1C1.
(2)画出△ABC关于点O的中心对称图形△A2B2C2.
(3)△A1B1C1与△A2B2C2组成的图形是轴对称图形吗?如果是,请画出对称轴.△A1B1C1与△A2B2C2组成的图形 (填“是”或“不是”)轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,求∠A+∠AEC+∠C的度数.
解:过点E作EF∥AB.
∵EF∥AB(已作)
∴∠A+∠AEF=180°(______)
又∵AB∥CD(已知)
∴EF∥CD(______)
∴∠CEF+∠______=180°(两直线平行,同旁内角互补)
∴∠A+∠AEF+∠CEF+∠C=360°(等式性质)
即∠A+∠AEC+∠C=______.
(2)根据上述解题及作辅助线的方法,在图2中,AB∥EF,则∠B+∠C+∠D+∠E=______.
(3)根据(1)和(2)的规律,图3中AB∥GF,猜想:∠B+∠C+∠D+∠E+∠F=______.
(4)如图4,AB∥CD,在B,D两点的同一侧有M1,M2,M3,…Mn共n个折点,则∠B+∠M1+∠M2+…+∠Mn+∠D的度数为______(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2ax+c的图象与x轴交于A、B两点(点A在点B的左边)AB=4,与y轴交于点C,OC=OA,点D为抛物线的顶点.
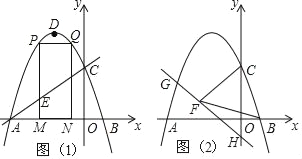
(1)求抛物线的解析式;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM,如图1,点P在点Q左边,当矩形PQNM的周长最大时,求m的值,并求出此时的△AEM的面积;
(3)已知H(0,﹣1),点G在抛物线上,连HG,直线HG⊥CF,垂足为F,若BF=BC,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解学生每天完成家庭作业所用时间的情况,从每班抽取相同数量的学生进行调查,并将所得数据进行整理,制成条形统计图和扇形统计图,如图所示:


(1)补全条形统计图;
(2)求扇形统计图中扇形D的圆心角的度数;
(3)若该中学有2000名学生,请估计其中有多少名学生能在1.5 h内完成家庭作业.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com