
【题目】如图,抛物线y=ax2+2ax+c的图象与x轴交于A、B两点(点A在点B的左边)AB=4,与y轴交于点C,OC=OA,点D为抛物线的顶点.
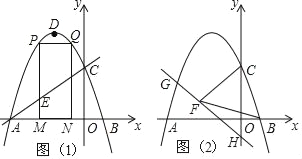
(1)求抛物线的解析式;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM,如图1,点P在点Q左边,当矩形PQNM的周长最大时,求m的值,并求出此时的△AEM的面积;
(3)已知H(0,﹣1),点G在抛物线上,连HG,直线HG⊥CF,垂足为F,若BF=BC,求点G的坐标.
【答案】(1)y=﹣x2﹣2x+3; (2)m=﹣2, ![]() ;
;
(3)点G的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).
【解析】试题分析:(1)根据抛物线y=ax2+2ax+c,可得C(0,c),对称轴为x﹣1,再根据OC=OA,AB=4,可得A(﹣3,0),最后代入抛物线y=ax2+2ax+3,得抛物线的解析式为y=﹣x2﹣2x+3;
(2)根据点M(m,0),可得矩形PQNM中,P(m,﹣m2﹣2m+3),Q(﹣2﹣m,﹣m2﹣2m+3),再根据矩形PQNM的周长=2(PM+PQ)=﹣2(m+2)2+10,可得当m=﹣2时,矩形PQNM的周长有最大值10,M的坐标为(﹣2,0),最后由直线AC为y=x+3,AM=1,求得E(﹣2,1),ME=1,据此求得△AEM的面积;
(3)连接CB并延长,交直线HG与Q,根据已知条件证明BC=BF=BQ,再根据C(0,3),B(1,0),得出Q(2,﹣3),根据H(0,﹣1),求得QH的解析式为y=﹣x﹣1,最后解方程组![]() ,可得点G的坐标.
,可得点G的坐标.
试题解析:(1)由抛物线y=ax2+2ax+c,可得C(0,c),对称轴为x=﹣![]() =﹣1,
=﹣1,
∵OC=OA,
∴A(﹣c,0),B(﹣2+c,0),
∵AB=4,
∴﹣2+c﹣(﹣c)=4,
∴c=3,
∴A(﹣3,0),
代入抛物线y=ax2+2ax+3,得
0=9a﹣6a+3,
解得a=﹣1,
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)如图1,
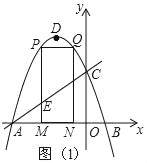
∵M(m,0),PM⊥x轴,
∴P(m,﹣m2﹣2m+3),
又∵对称轴为x=﹣1,PQ∥AB,
∴Q(﹣2﹣m,﹣m2﹣2m+3),
又∵QN⊥x轴,
∴矩形PQNM的周长
=2(PM+PQ)
=2[(﹣m2﹣2m+3)+(﹣2﹣m﹣m)]
=2(﹣m2﹣4m+1)
=﹣2(m+2)2+10,
∴当m=﹣2时,矩形PQNM的周长有最大值10,
此时,M(﹣2,0),
由A(﹣3,0),C(0,3),可得
直线AC为y=x+3,AM=1,
∴当x=﹣2时,y=1,即E(﹣2,1),ME=1,
∴△AEM的面积=![]() ×AM×ME=
×AM×ME=![]() ×1×1=
×1×1=![]() ;
;
(3)如图2,连接CB并延长,交直线HG与Q,
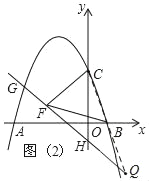
∵HG⊥CF,BC=BF,
∴∠BFC+∠BFQ=∠BCF+∠Q=90°,∠BFC=∠BCF,
∴∠BFQ=∠Q,
∴BC=BF=BQ,
又∵C(0,3),B(1,0),
∴Q(2,﹣3),
又∵H(0,﹣1),
∴QH的解析式为y=﹣x﹣1,
解方程组![]() ,可得
,可得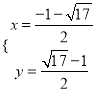 或
或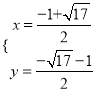 ,
,
∴点G的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代的数学专著,是“算经十书”(汉唐之间出现的十部古算书)中最重要的一种.书中有下列问題:“今有邑方不知大小,各中开门,出北门八十步有木,出西门二百四十五步见木,问邑方有几何?”意思是:如图,点![]() 、点
、点![]() 分别是正方形
分别是正方形![]() 的边
的边![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() 过点
过点![]() ,
,![]() 步,
步,![]() 步,则正方形的边长为( )
步,则正方形的边长为( )

A.![]() 步B.
步B.![]() 步C.
步C.![]() 步D.
步D.![]() 步
步
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,弦CD⊥AB于E,∠CDB=15°,OE=2![]() .
.
(1)求⊙O的半径;
(2)将△OBD绕O点旋转,使弦BD的一个端点与弦AC的一个端点重合,则弦BD与弦AC的夹角为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知∠A=∠F,∠C=∠D,试说明:BD∥CE.
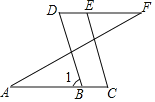
解:∵∠A=∠F(已知)
∴AC∥DF(______)
∴∠D=∠1(______)
又∵∠C=∠D(已知)
∴∠1=______
∴BD∥CE(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取一部分同学就“我最喜爱的体育项目”进行了一次抽样调查,下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
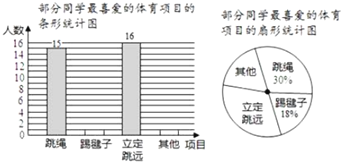
(1)小龙共抽取______名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“其他”部分对应的圆心角的度数是_______;
(4)若全校共2100名学生,请你估算“立定跳远”部分的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC.
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=_____度;
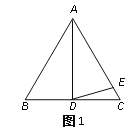
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=_______度;
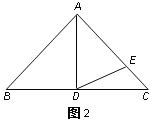
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:____________________.
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.
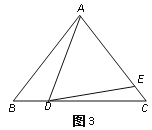
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com