【题目】在大课间活动中，同学们积极参加体育锻炼，小龙在全校随机抽取一部分同学就“我最喜爱的体育项目”进行了一次抽样调查，下面是他通过收集的数据绘制的两幅不完整的统计图，请你根据图中提供的信息，解答以下问题：
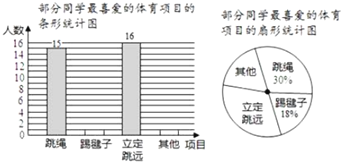
(1)小龙共抽取______名学生；
(2)补全条形统计图；
(3)在扇形统计图中，“其他”部分对应的圆心角的度数是_______；
(4)若全校共2100名学生，请你估算“立定跳远”部分的学生人数.
【答案】(1)50；(2)补图见解析；(3)72°；(4)672人.
【解析】
(1)画出统计图,根据跳绳的人数除以占的百分比即可得出抽取的学生总数;
(2)根据总学生数,求出踢毽子与其中的人数,补全条形统计图即可
(3)根据立定跳远占的百分比乘以360即可得到结果
(4)由其他占的百分比,乘以2100即可得到结果
(1)根据题意得:15÷30%=50(名)
则小明共抽取50名学生
(2)根据题意得:踢毽子人数为50×18%=9(名),其
他人数为50×(1-30%-18%-32%)=10名),
补全条形统计图,如图所示
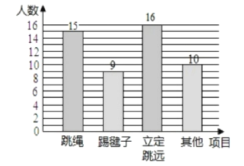
(3)根据题意得:360°×20%=72°
则“其他"部分对应的圆心角的度数是72°;
(4)根据题意得'其他"部分的学生有
2100×32%=672(名)
科目：初中数学 来源： 题型：
【题目】在①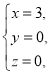
②
③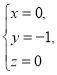
这三对数值中，__________是方程x＋2y＋z＝3的解，__________是方程2x－y－z＝1的解，__________是方程3x－y－z＝2的解，因此__________是方程组
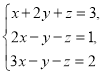的解．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+2ax+c的图象与x轴交于A、B两点（点A在点B的左边）AB=4，与y轴交于点C，OC=OA，点D为抛物线的顶点．
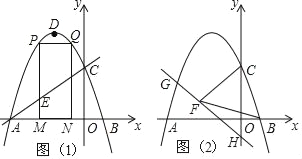
（1）求抛物线的解析式；
（2）点M（m，0）为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，可得矩形PQNM，如图1，点P在点Q左边，当矩形PQNM的周长最大时，求m的值，并求出此时的△AEM的面积；
（3）已知H（0，﹣1），点G在抛物线上，连HG，直线HG⊥CF，垂足为F，若BF=BC，求点G的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：BC∥OA，∠B=∠A=120°，试回答下列问题：
(1)如图1所示，求证：OB∥AC；
(2)如图2，若点E、F在BC上，且满足∠FOC=∠AOC，并且OE平分∠BOF，则∠EOC的度数是______；
(3)在(2)的条件下，若平行移动AC，其它条件不变，如图3，则∠OCB：∠OFB的值是______．
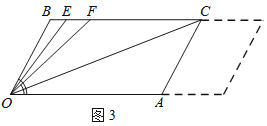
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，已知△ABC中，P是边AB上的一点，连接CP．
（1）要使△ACP∽△ABC，还需要补充的一个条件是_____．
（2）若△ACP∽△ABC，且AC=
，AB=3，求AP的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，点A（﹣3，0），点B是x轴上异于点A一动点，设B（x，0），以AB为边在x轴的上方作正方形ABCD．
（1）如图（1），若点B（1，0），则点D的坐标为 ；
（2）若点E是AB的中点，∠DEF＝90°，且EF交正方形外角的平分线BF于F．
①如图（2），当x＞0时，求证：DE＝EF；
②若点F的纵坐标为y，求y关于x的函数解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学为了了解学生每天完成家庭作业所用时间的情况，从每班抽取相同数量的学生进行调查，并将所得数据进行整理，制成条形统计图和扇形统计图，如图所示：
(1)补全条形统计图；
(2)求扇形统计图中扇形D的圆心角的度数；
(3)若该中学有2000名学生，请估计其中有多少名学生能在1.5 h内完成家庭作业．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在⊙O中，AB是⊙O的直径，AB=10， 
，点E是点D关于AB的对称点，M是AB上的一动点，下列结论：①∠BOE=60°；②∠CED=
∠AOD；③DM⊥CE；④CM+DM的最小值是10，其中正确的序号是______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
