
【题目】在一节数学实践活动课上,老师拿出三个边长都为5cm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.

【答案】(1) ![]() ;
; ![]() ;
; ![]() ;(2)
;(2) ![]()
【解析】试题分析:(1)(Ⅰ)观察图形可知:图①能盖住三个正方形所需的圆形硬纸板最小直径=三个正方形组成的矩形的对角线长,利用勾股定理可求出结果;(Ⅱ)图②中圆形硬纸板的半径是正方形的对角线长,利用勾股定理可求出结果;(Ⅲ)图③中圆形硬纸板的直径是正方形的对角线长的2倍,利用勾股定理可求出结果;(2)把三个正方形摆成“品”字形时,形硬纸板的直径最小,根据勾股定理解答即可.
试题解析:(1)(Ⅰ)观察图形可知:图①能盖住三个正方形所需的圆形硬纸板最小直径=三个正方形组成的矩形的对角线长=![]() ;(Ⅱ)图②中圆形硬纸板的半径=正方形的对角线长=
;(Ⅱ)图②中圆形硬纸板的半径=正方形的对角线长=![]() ,所以直径=
,所以直径=![]() ;(Ⅲ)图③中圆形硬纸板的直径=正方形的对角线长的2倍=
;(Ⅲ)图③中圆形硬纸板的直径=正方形的对角线长的2倍=![]() ;
;
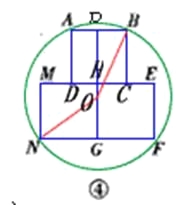
(2)如图④为盖住三个正方形时直径最小的放置方法
连接OB,ON,延长OH交AB于点P,则OP⊥AB,P为AB中点设OG=x,则OP=8-x
则有:, ![]()
解得:x=![]()
则ON=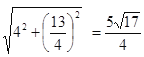 ,∴直径为
,∴直径为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读材料,理解应用:
已知方程x2+x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x,所以x=![]() .把x=
.把x=![]() 代入已知方程,得(
代入已知方程,得(![]() )2+
)2+![]() ﹣1=0.
﹣1=0.
化简,得:y2+2y﹣4=0.这种利用方程根的代替求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化成一般形式);
(1)已知方程x2+x﹣2=0,求一个一元二次方程,使它的根分别是已知方程根的相反数.
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,属于真命题的是( )
A. 同位角互补B. 多边形的外角和小于内角和
C. 平方根等于本身的数是1D. 同一平面内,垂直于同一条直线的两条直线平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com