
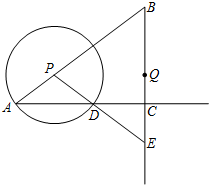
 如图,在Rt∠ABC中,∠ACB=90°,AC=8,tanB=$\frac{4}{3}$,点P是线段AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为点D,射线PD交射线BC于点E,点Q是线段BE的中点.
如图,在Rt∠ABC中,∠ACB=90°,AC=8,tanB=$\frac{4}{3}$,点P是线段AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为点D,射线PD交射线BC于点E,点Q是线段BE的中点.分析 (1)过点P作PH⊥AD,垂足为点H,利用已知条件以及勾股定理可分别得到PH,AH,AD,CD的长,再由PH∥BE,可得$\frac{PH}{CE}=\frac{DH}{CD}$,所以$\frac{\frac{3x}{5}}{y}=\frac{\frac{4x}{5}}{8-\frac{8x}{5}}$,进而可求出y关于x的函数关系式;
(2)首先利用已知条件得到BQ,PQ的长,再分两种情况:①当⊙Q和⊙P外切时,②当⊙Q和⊙P内切时,分别讨论求出⊙P的半径即可;
(3)当△PMC是等腰三角形,存在以下几种情况:①当MP=MC=x时,②当CP=CM时,③当PM=PC=x时,分别讨论求出符合题意的x值即可得到AP的长.
解答 解:(1)过点P作PH⊥AD,垂足为点H,
∵∠ACB=90°,tanB=$\frac{4}{3}$,
∴sinA=$\frac{3}{5}$,
∵PA=x,
∴PH=$\frac{3}{5}$x,
∵∠PHA=90°,
∴PH2+AH2=PA2,
∴AH=$\frac{4}{5}$x.
∵在⊙P中,PH⊥弦AD,
∴DH=AH=$\frac{4}{5}$x,
∴AD=$\frac{8}{5}$x,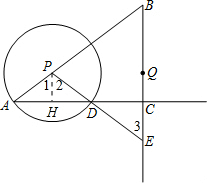
又∵AC=8,
∴CD=8-$\frac{8}{5}$x,
∵∠PHA=∠BCA=90°,
∴PH∥BE,
∴$\frac{PH}{CE}=\frac{DH}{CD}$,
∴$\frac{\frac{3x}{5}}{y}=\frac{\frac{4x}{5}}{8-\frac{8x}{5}}$,
∴y=6-$\frac{6}{5}$x(0<x<5);
(2)∵PA=PD,PH⊥AD,
∴∠1=∠2,
∵PH∥BE,
∴∠1=∠B,∠2=∠3,
∴PB=PE,
∵Q是BE的中点,
∴PQ⊥BE,
∴tanB=$\frac{PQ}{BQ}$=$\frac{4}{3}$,
∴cosB=$\frac{BQ}{BP}=\frac{3}{5}$,
∵PA=x,
∴PB=10-x,
∴BQ=6-$\frac{3}{5}$x,PQ=8-$\frac{4}{5}$x,
①当⊙Q和⊙P外切时:PQ=AP+BQ
∴8-$\frac{4}{5}$x=x+6-$\frac{3}{5}$x,
∴x=$\frac{5}{3}$;
②当⊙Q和⊙P内切时,此时⊙P的半径大于⊙Q的半径,则PQ=AP-BQ,
∴8-$\frac{4}{5}$x=x-(6-$\frac{3}{5}$x),
∴x=$\frac{35}{6}$,
∴当⊙Q和⊙P相切时,⊙P的半径为$\frac{5}{3}$或$\frac{35}{6}$.
(3)当△PMC是等腰三角形,存在以下几种情况:
①当MP=MC=x时,
∵QC=6-(6-$\frac{3}{5}$x)=$\frac{3}{5}$x,
∴MQ=$\frac{4}{5}$x,
若M在线段PQ上时,PM+MQ=PQ,
∴x+$\frac{4}{5}$x=8-$\frac{4}{5}$x,
∴x=$\frac{40}{13}$;
若M在线段PQ的延长线上时,PM-MQ=PQ,
∴x-$\frac{4}{5}$x=8-$\frac{4}{5}$x,
∴x=8;
②当CP=CM时,
∵CP=CM,CQ⊥PM,
∴PQ=QM=$\frac{1}{2}$PM=$\frac{1}{2}$x,
∴x-$\frac{4}{5}$x=$\frac{1}{2}$x,
∴x=$\frac{80}{13}$,
③当PM=PC=x时,
∵AP=x,
∴PA=PC,
又∵PH⊥AC,
∴AH=CH,
∵PH∥BE,
∴$\frac{AP}{BP}=\frac{AH}{CH}=1$,
∴$\frac{x}{10-x}=1$,
∴x=5.
综上所述:当△PMC是等腰三角形时,AP的长为$\frac{40}{13}$或$\frac{80}{13}$或5或8.
点评 本题考查了圆的综合题:熟练掌握两圆相切的性质和三角形相似的判定与性质;会运用勾股定理和相似比进行几何计算;能运用分类讨论的思想解题是答题关键,题目的综合性很强,牵扯到的知识点较多,对学生的综合解题能力要求很高.


科目:初中数学 来源: 题型:解答题
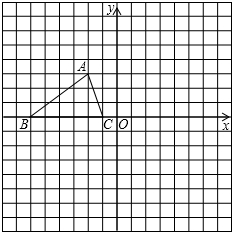 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)B(-6,0),C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 人数(人) 答对的题数(道) 班级 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 甲班 | 0 | 1 | 1 | 3 | 4 | 11 | 16 | 12 | 2 |
| 乙班 | 0 | 1 | 0 | 2 | 5 | 12 | 15 | 13 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com