
| 人数(人) 答对的题数(道) 班级 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 甲班 | 0 | 1 | 1 | 3 | 4 | 11 | 16 | 12 | 2 |
| 乙班 | 0 | 1 | 0 | 2 | 5 | 12 | 15 | 13 | 2 |
分析 (1)根据众数的定义,结合表格信息即可得出答案;
(2)先求出大于或等于7道的人数,继而根据优秀率=优秀人数÷总数即可得出答案;
(3)列出这两个人所在的班级情况,从而计算即可.
解答 解:(1)由表格可得,甲班答对6道题的人数最多,即甲班学生答对的题数的众数是6;
故答案为:6;
(2)乙班答对的题数大于或等于7道的人数有:13+2=15,
故优秀率为:$\frac{15}{50}$=30%;
(3)设甲班答题全对的两个人为A和B,乙班答题全对的两个人为C和D,
随机抽取2人的情况共有A和B、A和C、A和D、B和C、B和D、C和D共6种,
而抽到的2人在同一个班级的情况有A和B、C和D这2种,
故可得抽到的2人在同一个班级的概率=$\frac{2}{6}$=$\frac{1}{3}$.
故答案为:6,30%,$\frac{1}{3}$.
点评 本题考查了众数、统计表及树状图求概率的知识,解答本题的关键是能准确读图,从表格中得到解题需要的信息,难度一般


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:| 三角形ABC | A(a,2) | B(-5,1) | C(-2,0) |
| 三角形A′B′C′ | A′(3,4) | B′(1,b) | C′(c,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
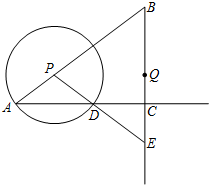 如图,在Rt∠ABC中,∠ACB=90°,AC=8,tanB=$\frac{4}{3}$,点P是线段AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为点D,射线PD交射线BC于点E,点Q是线段BE的中点.
如图,在Rt∠ABC中,∠ACB=90°,AC=8,tanB=$\frac{4}{3}$,点P是线段AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为点D,射线PD交射线BC于点E,点Q是线段BE的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{2}{3}}$=$\frac{\sqrt{2}}{3}$ | B. | $\sqrt{40}$=5$\sqrt{8}$ | C. | $\sqrt{\frac{8}{9}}$=$\frac{4\sqrt{2}}{3}$ | D. | 8$\sqrt{\frac{3}{2}}$=4$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (6,9) | C. | (0,-1) | D. | (9,6) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\root{3}{2}$ | C. | $\sqrt{4}$ | D. | $\sqrt{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com