练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．已知直角三角形的两条边边长分别为15和25，则第三边长为20或5$\sqrt{34}$．

    分析 此题有两种情况，一是当这个直角三角形的斜边的长为25时，求另一条直角边的长；二是当这个直角三角形两条直角边的长分别为15、25时，求斜边的长．然后根据勾股定理即可求得答案．

    解答 解：当这个直角三角形的斜边的长为5时，
    第三边的长=$\sqrt{{25}^{2}-{15}^{2}}$=20；
    当这个直角三角形两条直角边的长分别为5、4时，
    第三边的长=$\sqrt{{25}^{2}+{15}^{2}}$=5$\sqrt{34}$．
    故答案为：20或5$\sqrt{34}$．

    点评 本题主要考查学生对勾股定理的理解和掌握，解答此题的关键是结合勾股定理运用分类讨论的思想，分析该题有两种情况．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    7．把a2b-2ab2+b3分解因式正确的是（　　）
    A．b（a2-2ab+b2）B．a2b-b2（2a-y）C．b（a-b）2D．b（a+b）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图，AB∥DE，若∠1=45°，则∠2=135°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．十二届全国人大三次会议上国务院总理李克强作政府工作报告中提到，去年我国城镇新增就业1322万人，把1322万用科学记数法表示应是（　　）
    A．13.22×106B．1.322×107C．1.322×103D．0.1322×108

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．李明同学开发了一种数值转换程序，当任意实数对（a，b）进入其中时，会得到一个新的实数：a-1+|b|-π0，例如把（3，-1）放入其中，就会的到3-1+|-1|-π0=$\frac{1}{3}$．现将实数对（-1，3）放入其中，得到实数m，再将实数对（m，2）放入其中，得到实数是2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

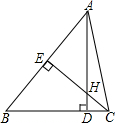    2．如图，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，已知∠B=48°，∠BAC=72°，求∠CAD与∠DHE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，P是⊙O外一点，A、B、C是⊙O上的三点，∠AOB=60°，PA、PB分别交$\widehat{ACB}$于M、N两点，则∠APB的范围是0°＜∠APB＜30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知25x=2000，80y=2000，则$\frac{xy}{x+y}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：（5+1）（52+1）（54+1）（58+1）…（564+1）

    查看答案和解析>>

    同步练习册答案