
【题目】如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).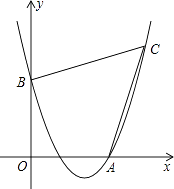
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边形AOBC的顶点重合)若能,求出DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
【答案】
(1)
解:设该抛物线的解析式为y=ax2+bx+c,
根据题意得 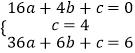 ,解得
,解得 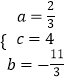 ,
,
∴抛物线的表达式为y= ![]() x2﹣
x2﹣ ![]() x+4
x+4
(2)
证明:如图1,连结AB、OC,

∵A(4,0),B(0,4),C(6,6),
∴OA=4,OB=4,CB= ![]() =2
=2 ![]() ,CA=
,CA= ![]() =2
=2 ![]() ,
,
∴OA=OB,CA=CB,
∴OC垂直平分AB,
即四边形AOBC的两条对角线互相垂直
(3)
解:能.
如图2,
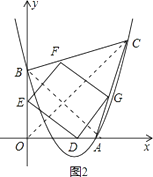
AB= ![]() =4
=4 ![]() ,OC=
,OC= ![]() =6
=6 ![]() ,设D(t,0),
,设D(t,0),
∵四边形DEFG为平行四边形,
∴EF∥DG,EF=DG,
∵OC垂直平分AB,
∴△OBC与△OAC关于OC对称,
∴EF和DG为对应线段,
∴四边形DEFG为矩形,DG∥OC,
∴DE∥AB,
∴△ODE∽△OAB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得DE=
,解得DE= ![]() t,
t,
∵DG∥OC,
∴△ADG∽△AOC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得DG=
,解得DG= ![]() (4﹣t),
(4﹣t),
∴矩形DEFG的面积=DEDG= ![]() t
t ![]() (4﹣t)=﹣3t2+12t=﹣3(t﹣2)2+12,
(4﹣t)=﹣3t2+12t=﹣3(t﹣2)2+12,
当t=2时,平行四边形DEFG的面积最大,最大值为12,此时D点坐标为(2,0).
【解析】(1)根据抛物线经过点A(4,0),B(0,4),C(6,6),利用待定系数法,求出抛物线的表达式即可;(2)利用两点间的距离公式分别计算出OA=4,OB=4,CB=2 ![]() ,CA=2
,CA=2 ![]() ,则OA=OB,CA=CB,根据线段垂直平分线定理的逆定理得到OC垂直平分AB,所以四边形AOBC的两条对角线互相垂直;(3)如图2,利用两点间的距离公式分别计算出AB=4
,则OA=OB,CA=CB,根据线段垂直平分线定理的逆定理得到OC垂直平分AB,所以四边形AOBC的两条对角线互相垂直;(3)如图2,利用两点间的距离公式分别计算出AB=4 ![]() ,OC=6
,OC=6 ![]() ,设D(t,0),根据平行四边形的性质四边形DEFG为平行四边形得到EF∥DG,EF=DG,再由OC垂直平分AB得到△OBC与△OAC关于OC对称,则可判断EF和DG为对应线段,所以四边形DEFG为矩形,DG∥OC,则DE∥AB,于是可判断△ODE∽△OAB,利用相似比得DE=
,设D(t,0),根据平行四边形的性质四边形DEFG为平行四边形得到EF∥DG,EF=DG,再由OC垂直平分AB得到△OBC与△OAC关于OC对称,则可判断EF和DG为对应线段,所以四边形DEFG为矩形,DG∥OC,则DE∥AB,于是可判断△ODE∽△OAB,利用相似比得DE= ![]() t,接着证明△ADG∽△AOC,利用相似比得DG=
t,接着证明△ADG∽△AOC,利用相似比得DG= ![]() (4﹣t),所以矩形DEFG的面积=DEDG=
(4﹣t),所以矩形DEFG的面积=DEDG= ![]() t
t ![]() (4﹣t)=﹣3t2+12t,然后根据二次函数的性质求平行四边形DEFG的面积的最大值,从而得到此时D点坐标.
(4﹣t)=﹣3t2+12t,然后根据二次函数的性质求平行四边形DEFG的面积的最大值,从而得到此时D点坐标.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.则ABCD的周长为_____,面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示﹣3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.如果表示数a和﹣2的两点之间的距离是3,那么a= ;
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a取何值时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值是多少?请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
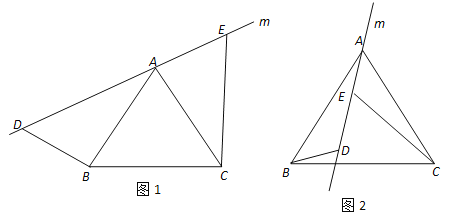
【题目】探索与证明:(1)如图1,直线m经过正三角形ABC的顶点A,在直线m上取两点 D,E,使得∠ADB=60°,∠AEC=60°.通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明;
(2)将(1)中的直线m绕点A逆时针方向旋转一个角度到如图2的位置,并使∠ADB=120°,∠AEC=120°.通过观察或测量,请直接写出线段BD,CE与DE之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF. 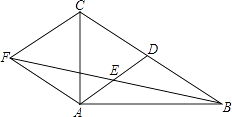
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据![]() 中华人民共和国2017年国民经济和社会发展统计公报
中华人民共和国2017年国民经济和社会发展统计公报![]() ,我国
,我国![]() 年农村贫困人口统计如图所示
年农村贫困人口统计如图所示![]() 根据统计图中提供的信息,预估2018年年末全国农村贫困人口约为______万人,你的预估理由是______.
根据统计图中提供的信息,预估2018年年末全国农村贫困人口约为______万人,你的预估理由是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com