
【题目】如图,在ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,BE=12cm,CE=5cm.则ABCD的周长为_____,面积为_____.

【答案】39cm60cm2
【解析】
根据角平分线的定义和平行线的性质得到等腰三角形ABE和等腰三角形CDE和直角三角形BCE.根据直角三角形的勾股定理得到BC=13cm,根据等腰三角形的性质得到AB=CD=![]() AD=
AD=![]() CD=6.5cm,从而求得该平行四边形的周长;根据直角三角形的面积可以求得平行四边形BC边上的高.
CD=6.5cm,从而求得该平行四边形的周长;根据直角三角形的面积可以求得平行四边形BC边上的高.
∵BE、CE分别平分∠ABC、∠BCD,
∴∠1=∠3=![]() ∠ABC,∠DCE=∠BCE=
∠ABC,∠DCE=∠BCE=![]() ∠BCD,
∠BCD,
∵AD∥BC,AB∥CD,
∴∠2=∠3,∠BCE=∠CED,∠ABC+∠BCD=180°,
∴∠1=∠2,∠DCE=∠CED,∠3+∠BCE=90°,
∴AB=AE,CD=DE,∠BEC=90°,
在Rt△BCE中,根据勾股定理得:BC=13cm,
根据平行四边形的对边相等,得到:AB=CD,AD=BC,
∴平行四边形的周长等于:AB+BC+CD+AD=6.5+13+6.5+13=39cm;
作EF⊥BC与F,根据直角三角形的面积公式得:EF=![]() cm,
cm,
∴S平行四边形ABCD=BC·EF=![]() =60cm2,
=60cm2,
故答案为:39cm,60cm2.


科目:初中数学 来源: 题型:
【题目】2017年体育中考在即,学校体育组对九(1)班50名学生进行了长跑项目的测试,根据测试成绩制作了如图两个统计图.
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少?
(3)该校九年级共有600名学生参加了长跑项目的测试,估计测试成绩在4分以上(含4分)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全球气候变暖导致-些冰川融化并消失,在冰川|消失12年后,一种低等植物苔藓,就开始在岩石上生长,每一个苔藓都会长成近似的圆形,苔藓的直径和其生长年限近似地满足如下的关系式:d=7![]() (t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。
(t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。
(1)计算冰川消失16年后苔藓的直径为多少厘米?
(2)如果测得一些苔藓的直径是35厘米,问冰川约是在多少年前消失的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是平行四边形ABCD的对角线,E、H分别为边BA和边BC延长线上的点,连接EH交AD、CD于点F、G,且EH∥AC.
(1)求证:EG=FH;
(2)若△ACD是等腰直角三角形,∠ACD=90°,F是AD的中点,AD=6,连接BF,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图像与反比例函数y= ![]() 的图像交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图像交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D. 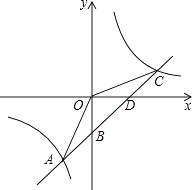
(1)求反比例函数y= ![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.、
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,…,则第⑥个图形中五角星的个数为( )
A.50
B.64
C.68
D.72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).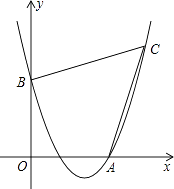
(1)求抛物线的表达式;
(2)证明:四边形AOBC的两条对角线互相垂直;
(3)在四边形AOBC的内部能否截出面积最大的DEFG?(顶点D,E,F,G分别在线段AO,OB,BC,CA上,且不与四边形AOBC的顶点重合)若能,求出DEFG的最大面积,并求出此时点D的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com