Question

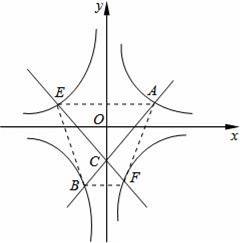
如图，在平面直角坐标系中，双曲线y=与一次函数y=kx+b（k＞0）分别交于点A与点B，直线与y轴交于点C，把直线AB绕着点C旋转一定的角度后，得到一条新直线．若新直线与双曲线y=﹣相交于点E、F，并使得双曲线y=，y=﹣，连线y=kx+b以及新直线构成的图形能关于某条坐标轴对称，如果点A的横坐标为1，则当k为多少时，点A、点E、点B、点F构成的四边形的面积最小．最小值是多少？

Answer 1

【考点】反比例函数综合题．

【分析】将A横坐标代入反比例y=中，求出y的值确定出A的纵坐标，将A坐标代入y=kx+b中表示出b，得到一次函数解析式，与反比例解析式联立，消去y得到关于x的一元二次方程，求出方程的解表示出B坐标，由双曲线y=与y=﹣与直线y=kx+b以及新直线的对称性可得：点A与点E关于y轴对称，点B与点F关于y轴对称，表示出E与F坐标，进而确定出AE与BF，且AE与BF的距离为k+1，利用梯形的面积公式表示出梯形AEBF的面积即可．

【解答】解：∵x_A=1，A点在y=上，

∴y_A=1，

把点A（1，1）代入y=kx+b中得：1=k+b，

∴b=1﹣k，

∴y=kx+（1﹣k），

由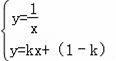，消去y得： =kx+（1﹣k），

整理得：kx²+（1﹣k）x﹣1=0，

∴x₁=1，x₂=﹣，

∴点B的坐标为（﹣，﹣k），

由双曲线y=与y=﹣与直线y=kx+b以及新直线的对称性可得：

点A与点E关于y轴对称，点B与点F关于y轴对称，

∴E（﹣1，1）、F（，﹣k），

∴AE=2，BF=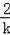，AE与BF的距离为k+1，

∴S_梯形AEBF=（k+1）=（1+）（k+1）=k++2，

∵k＞0∴当k=1时，梯形S_AEBF有最小值4．

【点评】此题属于反比例函数综合题，涉及的知识有：待定系数法确定函数解析式，一次函数与反比例函数的交点，坐标与图形性质，以及对称的性质，由双曲线y=与y=﹣与直线y=kx+b以及新直线的对称性可得：点A与点E关于y轴对称，点B与点F关于y轴对称是解本题的关键．