
【题目】如图,![]() ,点
,点![]() 分别在
分别在![]() 直线上,点
直线上,点![]() 为两平行线内部一点
为两平行线内部一点

(1)如图1,![]() 角平分线交于点N,若
角平分线交于点N,若![]() 等于
等于![]() ,求
,求![]() 的度数
的度数
(2)如图2,点G为直线![]() 上一点,且
上一点,且![]() ,延长GM交直线AB于点Q,点P为MG上一点,射线
,延长GM交直线AB于点Q,点P为MG上一点,射线![]() 相交于点H,满足
相交于点H,满足![]() ,设
,设![]() ,求
,求![]() 的度数(用
的度数(用![]() 的代数式表示)
的代数式表示)
【答案】(1)115°;(2)∠H=60°-![]() α.
α.
【解析】
(1)过M作ME∥AB,利用平行线的性质以及角平分线的定义计算即可.
(2)如图②中设∠BEH=x,∠PFG=y,则∠BEM=3x,∠MFG=3y,设EH交CD于K.证明∠H=x-y,求出x-y即可解决问题.
解:(1)过M作ME∥AB,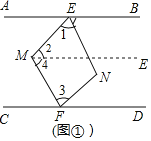
∵AB∥CD,
∴ME∥CD,
∴∠BEM+∠2=∠DFM+∠4=180°,
∴∠BEM=180°-∠2,∠DFM=180°-∠4,
∵EN,FN分别平分∠MEB和∠DFM,
∴∠1=![]() ∠BEM,∠3=
∠BEM,∠3=![]() ∠DFM,
∠DFM,
∴∠1+∠3=![]() (180°-∠2)+
(180°-∠2)+![]()
(180°-∠4)=180°-![]() (∠2+∠4)=180°-
(∠2+∠4)=180°-![]() ×130°=115°,
×130°=115°,
∴∠ENF=360°-∠1-∠3-∠EMF=360°-115°-130°=115°;
(2)如图②中设∠BEH=x,∠PFG=y,则∠BEM=3x,∠MFG=3y,设EH交CD于K.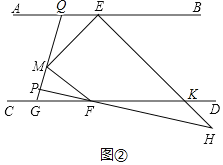
∵AB∥CD,
∴∠BEH=∠DKH=x,
∵∠PFG=∠HFK=y,∠DKH=∠H+∠HFK,
∴∠H=x-y,
∵∠EMF=∠MGF=α,∠BQG+∠MGF=180°,
∴∠BQG=180°-α,
∵∠QMF=∠QME+∠EMF=∠MGF+∠MFG,
∴∠QME=∠MFG=3y,
∵∠BEM=∠QME+∠MQE,
∴3x-3y=180°-α,
∴x-y=60°-![]() α,
α,
∴∠H=60°-![]() α.
α.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中.AB=AC.∠BAC=90![]() .E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
.E是AC边上的一点,延长BA至D,使AD=AE,连接DE,CD.
(l)图中是否存在两个三角形全等?如果存在请写出哪两个三角形全等,并且证明;如果不存在,请说明理由;
(2)若∠CBE=30![]() ,求∠ADC的度数.
,求∠ADC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF//AD, ∠1=∠2, ∠BAC=70°.求∠AGD的度数(将以下过程填写完整)

解:∵EF//AD
∴∠2=
又∵∠1=∠2
∴∠1=∠3
∴ AB//
∴∠BAC+ =180°.
又∵∠BAC=70°
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据说,我国著名数学家华罗庚在一次访问途中,看到飞机邻座的乘客阅读的杂志上有一道智力题:一个数32768,它是一个正数的立方,希望求它的立方根,华罗庚不假思索给出了答案,邻座乘客非常惊奇,很想得知其中的奥秘,你知道华罗庚是怎样准确计算出的吗?请按照下面的问题试一试:
(1)由![]() ,因为
,因为![]() ,请确定
,请确定![]() 是______位数;
是______位数;
(2)由32768的个位上的数是8,请确定![]() 的个位上的数是________,划去32768后面的三位数768得到32,因为
的个位上的数是________,划去32768后面的三位数768得到32,因为![]() ,请确定
,请确定![]() 的十位上的数是_____________
的十位上的数是_____________
(3)已知13824和![]() 分别是两个数的立方,仿照上面的计算过程,请计算:
分别是两个数的立方,仿照上面的计算过程,请计算:![]() =____;
=____;![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
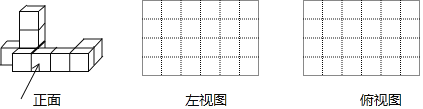
【题目】如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列题目.
(1)正面图中有______块小正方体;
(2)请在下面方格纸中分别画出它的左视图和俯视图(画出的图都用铅笔涂上阴影)
(3)用小正方体搭一个几何体,使得它的左视图和俯视图与你在(2)中所画的图一致,则这样的几何体最多要______块小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A.b≥ ![]()
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为开展“阳光体育”活动,计划拿出不超过3000元的资金购买一批篮球,羽毛球拍和乒乓球拍,已知篮球,羽毛球拍和乒乓球拍的单价比为8:3:2,且其单价和为130元,
(1)请问篮球,羽毛球拍和乒乓球拍的单价分别是多少元?
(2)若要求购买篮球,羽毛球拍和乒乓球拍的总数量是80个(副),羽毛球拍的数量是乒乓球拍数量的4倍,且购买乒乓球拍的数量不超过15副请问有几种购买方案?哪种方案,才能使运费最少?最少运费是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com