
【题目】如图,A、D、B、E四点在同一条直线上,AD=BE,BC∥EF,BC=EF.

(1)求证:AC=DF;
(2)若CD为∠ACB的平分线,∠A=25°,∠E=71°,求∠CDF的度数.
【答案】(1)详见解析;(2)42°.
【解析】
(1)根据平行线的性质得到∠ABC=∠DEF,再结合题意根据SAS判断△ABC≌△DEF,根据全等三角形的性质即可得到答案;
(2)根据全等三角形的性质得到∠ABC=∠E=71°,∠A=∠FDE=25°,再根据角平分线的性质进行计算即可得到答案.
证明:(1)∵AD=BE
∴AB=DE
∵BC∥EF
∴∠ABC=∠DEF,且AB=BE,BC=EF
∴△ABC≌△DEF(SAS)
∴AC=DF
(2)∵△ABC≌△DEF
∴∠ABC=∠E=71°,∠A=∠FDE=25°
∴∠ACB=180°﹣∠A﹣∠ABC=84°
∵CD为∠ACB的平分线
∴∠ACD=42°=∠BCD
∵∠CDB=∠A+∠ACD=∠CDF+∠EDF
∴∠CDF=42°


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产![]() 辆自行车,平均每天生产
辆自行车,平均每天生产![]() 辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
![]() 根据记录可知前三天共生产________辆;
根据记录可知前三天共生产________辆;
![]() 产量最多的一天比产量最少的一天多生产________辆;
产量最多的一天比产量最少的一天多生产________辆;
![]() 该厂实行计件工资制,每辆车
该厂实行计件工资制,每辆车![]() 元,超额完成任务每辆奖
元,超额完成任务每辆奖![]() 元,少生产一辆扣
元,少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前小王花1200元从农贸市场购进批发价分别为每箱30元与50元的A,B两种水果进行销售,并分别以每箱35元与60元的价格出售,设购进A水果x箱,B水果y箱.
(1)让小王将水果全部售出共赚了215元,则小王共购进A、B水果各多少箱?
(2)若要求购进A水果的数量不得少于B水果的数量,则应该如何分配购进A, B水果的数量并全部售出才能获得最大利润,此时最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形一边长为12cm,那么它的两条对角线的长度可以是( )
A. 8cm和14cm B. 10cm 和14cm C. 18cm和20cm D. 10cm和34cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个工人师傅要将一个正方形ABCD的余料,修剪成四边形ABEF的零件,其中CE=![]() BC,F是CD的中点.
BC,F是CD的中点.
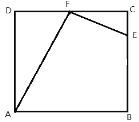
(1)若正方形的边长为a,试用含a的代数式表示AF2+EF2的值;
(2)连结AE,△AEF是直角三角形吗?为什么?(正方形的四条边都相等,四个角都是直角)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD=CE.
(1)如图1,求证:∠CAE=∠CBD;
(2)如图2,F是BD的中点,求证:AE⊥CF;
(3)如图3,F,G分别是BD,AE的中点,若AC=2![]() ,CE=1,求△CGF的面积.
,CE=1,求△CGF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
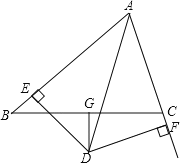
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)判断BE与CF的数量关系,并说明理由;
(2)如果AB=8,AC=6,求AE、BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com