
【题目】如图所示,一个工人师傅要将一个正方形ABCD的余料,修剪成四边形ABEF的零件,其中CE=![]() BC,F是CD的中点.
BC,F是CD的中点.
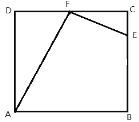
(1)若正方形的边长为a,试用含a的代数式表示AF2+EF2的值;
(2)连结AE,△AEF是直角三角形吗?为什么?(正方形的四条边都相等,四个角都是直角)
科目:初中数学 来源: 题型:
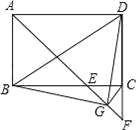
【题目】如图,在矩形![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() .其中正确的结论是______(填写所有正确结论的序号).
.其中正确的结论是______(填写所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接全国文明城市创建,市交警队的一辆警车在一条东西方向的公路上巡逻,如果规定向东为正,向西为负,从出发点开始所走的路程为:+2,-3,+2,+1,-2,-1,-2(单位:千米)
(1)最后,这辆警车的司机如何向队长描述他的位置?
(2)如果此时距离出发点东侧2千米处出现交通事故,队长命令他马上赶往现场处置,则警车在此次巡逻和处理事故中共耗油多少升?(已知每千米耗油0.2升)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、D、B、E四点在同一条直线上,AD=BE,BC∥EF,BC=EF.

(1)求证:AC=DF;
(2)若CD为∠ACB的平分线,∠A=25°,∠E=71°,求∠CDF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试根据图中信息,解答下列问题.

(1)一次性购买6根跳绳需_____元,一次性购买12根跳绳需______元;
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E.将△BDE沿直线DE折叠,得到△B′DE,若B′D,B′E分别交AC于点F,G,连接OF,OG,则下列判断错误的是( )
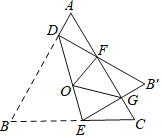
A. △ADF≌△CGE
B. △B′FG的周长是一个定值
C. 四边形FOEC的面积是一个定值
D. 四边形OGB'F的面积是一个定值
查看答案和解析>>
科目:初中数学 来源: 题型:
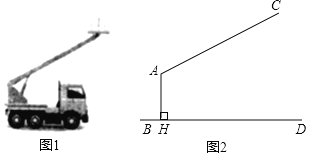
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:⊙O是正方形ABCD的外接圆,点E在![]() 上,连接BE、DE,点F在
上,连接BE、DE,点F在![]() 上连接BF、DF,BF与DE、DA分别交于点G、点H,且DA平分∠EDF.
上连接BF、DF,BF与DE、DA分别交于点G、点H,且DA平分∠EDF.
(1)如图1,求证:∠CBE=∠DHG;
(2)如图2,在线段AH上取一点N(点N不与点A、点H重合),连接BN交DE于点L,过点H作HK∥BN交DE于点K,过点E作EP⊥BN,垂足为点P,当BP=HF时,求证:BE=HK;
(3)如图3,在(2)的条件下,当3HF=2DF时,延长EP交⊙O于点R,连接BR,若△BER的面积与△DHK的面积的差为![]() ,求线段BR的长.
,求线段BR的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.
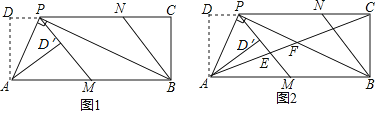
(1)求证:AD2=DPPC;
(2)请判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC,分别交PM,PB于点E,F.若![]() =
=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com