
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.
(1)求证:AD2=DPPC;
(2)请判断四边形PMBN的形状,并说明理由;
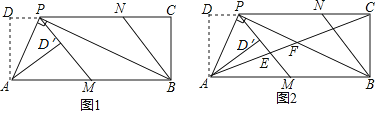
(3)如图2,连接AC,分别交PM,PB于点E,F.若![]() =
=![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)四边形PMBN是菱形,理由见解析;(3)![]()
【解析】(1)过点P作PG⊥AB于点G,易知四边形DPGA,四边形PCBG是矩形,所以AD=PG,DP=AG,GB=PC,易证△APG∽△PBG,所以PG2=AGGB,即AD2=DPPC;
(2)DP∥AB,所以∠DPA=∠PAM,由题意可知:∠DPA=∠APM,所以∠PAM=∠APM,由于∠APB-∠PAM=∠APB-∠APM,即∠ABP=∠MPB,从而可知PM=MB=AM,又易证四边形PMBN是平行四边形,所以四边形PMBN是菱形;
(3)由于![]() ,可设DP=k,AD=2k,由(1)可知:AG=DP=k,PG=AD=2k,从而求出GB=PC=4k,AB=AG+GB=5k,由于CP∥AB,从而可证△PCF∽△BAF,△PCE∽△MAE,从而可得
,可设DP=k,AD=2k,由(1)可知:AG=DP=k,PG=AD=2k,从而求出GB=PC=4k,AB=AG+GB=5k,由于CP∥AB,从而可证△PCF∽△BAF,△PCE∽△MAE,从而可得![]() ,
,![]() ,从而可求出EF=AF-AE=
,从而可求出EF=AF-AE=![]() AC-
AC-![]() AC=
AC=![]() AC,从而可得
AC,从而可得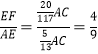 .
.
(1)过点P作PG⊥AB于点G,
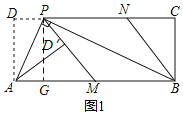
∴易知四边形DPGA,四边形PCBG是矩形,
∴AD=PG,DP=AG,GB=PC
∵∠APB=90°,
∴∠APG+∠GPB=∠GPB+∠PBG=90°,
∴∠APG=∠PBG,
∴△APG∽△PBG,
∴![]() ,
,
∴PG2=AGGB,
即AD2=DPPC;
(2)∵DP∥AB,
∴∠DPA=∠PAM,
由题意可知:∠DPA=∠APM,
∴∠PAM=∠APM,
∵∠APB-∠PAM=∠APB-∠APM,
即∠ABP=∠MPB
∴AM=PM,PM=MB,
∴PM=MB,
又易证四边形PMBN是平行四边形,
∴四边形PMBN是菱形;
(3)由于![]() ,
,
可设DP=k,AD=2k,
由(1)可知:AG=DP=k,PG=AD=2k,
∵PG2=AGGB,
∴4k2=kGB,
∴GB=PC=4k,
AB=AG+GB=5k,
∵CP∥AB,
∴△PCF∽△BAF,
∴![]() ,
,
∴![]() ,
,
又易证:△PCE∽△MAE,AM=![]() AB=
AB=![]() ,
,
∴![]()
∴![]() ,
,
∴EF=AF-AE=![]() AC-
AC-![]() AC=
AC=![]() AC,
AC,
∴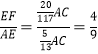 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,一个工人师傅要将一个正方形ABCD的余料,修剪成四边形ABEF的零件,其中CE=![]() BC,F是CD的中点.
BC,F是CD的中点.
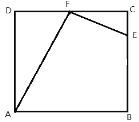
(1)若正方形的边长为a,试用含a的代数式表示AF2+EF2的值;
(2)连结AE,△AEF是直角三角形吗?为什么?(正方形的四条边都相等,四个角都是直角)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,b)、点B(a,0)、点D(d,0)且a、b、c满足![]() .DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
.DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
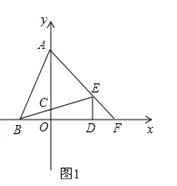
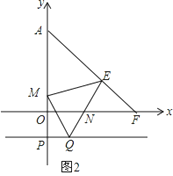
(1)求点A、B、D的坐标;
(2)求点C、E、F的坐标;
(3)如图,过P(0,-1)作x轴的平行线,在该平行线上有一点Q(点Q在P的右侧)使∠QEM=45°,QE交x轴于N,ME交y轴正半轴于M,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)判断BE与CF的数量关系,并说明理由;
(2)如果AB=8,AC=6,求AE、BE的长.
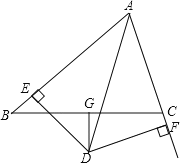
查看答案和解析>>
科目:初中数学 来源: 题型:
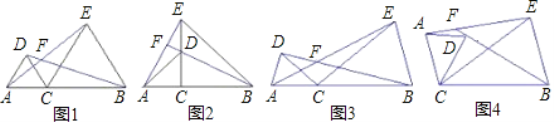
【题目】已知点C为线段AB上一点,分别以AC、BC为边在线段AB的同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.
(1)如图1,若∠ACD=60°,则∠AFB=______,如图2,若∠ACD=90°,则∠AFB=______,如图3,若∠ACD=α,则∠AFB=______(用含α的式子表示);
(2)设∠ACD=α,将图3中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),如图4,试探究∠AFB与α的数量关系,并予以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
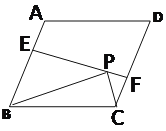
【题目】如图,在菱形ABCD中,sinD=![]() ,E、F分别是AB,CD上的点,BC=5,AE=CF=2,点P是线段EF上一点,则当△BPC时直角三角形时,CP的长为____________
,E、F分别是AB,CD上的点,BC=5,AE=CF=2,点P是线段EF上一点,则当△BPC时直角三角形时,CP的长为____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y1=![]() 与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
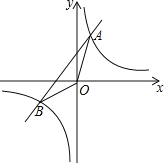
(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() x+b的解.
x+b的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张等边三角形纸片沿各边中点剪成4个小三角形,称为第一次操作;然后将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;……,根据以上操作,若要得到100个小三角形,则需要操作的次数是( )

A. 25 B. 33 C. 34 D. 50
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com