
【题目】在平面直角坐标系中,点A(0,b)、点B(a,0)、点D(d,0)且a、b、c满足![]() .DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
.DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
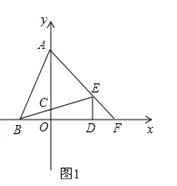
(1)求点A、B、D的坐标;
(2)求点C、E、F的坐标;
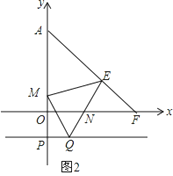
(3)如图,过P(0,-1)作x轴的平行线,在该平行线上有一点Q(点Q在P的右侧)使∠QEM=45°,QE交x轴于N,ME交y轴正半轴于M,求![]() 的值.
的值.
【答案】(1)A(0,3) B(-1,0) D(2,0);(2)![]() E(2,1) F(3,0);(3)
E(2,1) F(3,0);(3)![]()
【解析】
(1)由非负数的性质可求得a、b、d的值,可求得A、B、D的坐标;
(2)由条件可证明△ABO≌△BED,可求得DE和BD的长,可求得E点坐标,再求得直线AE与BE的解析式,可求得C、F点坐标;
(3)过E作EG⊥OA于点G,EH⊥PQ于点Q,可证明四边形GEHP为正方形,在GA上截GI=QH,可证明△IGE≌△QHE,可证得∠IEM=∠MEQ=45°,可证明△EIM≌△EQM,可得到IM=MQ,再结合条件可求得PH=AI=PQ,可求得答案.
解:(1)∵![]() ,
,
∴![]()
∴![]() ,
,
∴A(0,3),B(-1,0),D(2,0);
(2)∵A(0,3),B(-1,0),D(2,0),
∴OB=1,OD=2,OA=3,
∴AO=BD,
在△ABO和△BED中,
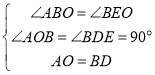 ,
,
∴△ABO≌△BED(AAS),
∴DE=BO=1,
∴E(2,1),
设直线AE解析式为:y=kx+b,直线BE解析式为:y=mx+n,如图1,

把点A、E代入y=kx+b,把点B、E代入y=mx+n,得
![]() ,
,![]() ,
,
解得:![]() ,
,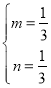 ,
,
∴直线AE解析式为:![]() ,
,
直线BE解析式为:![]() ,
,
∴直线![]() ,令
,令![]() ,解得:
,解得:![]() ,
,
∴点F为:![]() ,
,
∴直线![]() ,令
,令![]() ,解得:
,解得:![]() ,
,
∴点C为:![]() ;
;
(3)过E作EG⊥OA,EH⊥PQ,垂足分别为G、H,在GA上截取GI=QH,如图2,
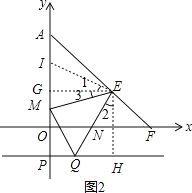
∵E(2,1),P(-1,0),
∴GE=GP=GE=PH=2,
∴四边形GEHP为正方形,
∴∠IGE=∠EHQ=90°,
在Rt△IGE和Rt△QHE中
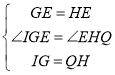 ,
,
∴△IGE≌△QHE(SAS),
∴IE=EQ,∠1=∠2,
∵∠QEM=45°,
∴∠2+∠3=45°,
∴∠1+∠3=45°,
∴∠IEM=∠QEM,
在△EIM和△EQM中,
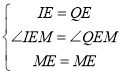 ,
,
∴△EIM=EQM(SAS),
∴IM=MQ,
∴AM-MQ=AM-IM=AI,
由(2)可知OA=OF=3,∠AOF=90°,
∴∠A=∠AEG=45°,
∴PH=GE=GA=IG+AI,
∴AI=GA-IG=PH-QH=PQ,
![]()


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】为了迎接全国文明城市创建,市交警队的一辆警车在一条东西方向的公路上巡逻,如果规定向东为正,向西为负,从出发点开始所走的路程为:+2,-3,+2,+1,-2,-1,-2(单位:千米)
(1)最后,这辆警车的司机如何向队长描述他的位置?
(2)如果此时距离出发点东侧2千米处出现交通事故,队长命令他马上赶往现场处置,则警车在此次巡逻和处理事故中共耗油多少升?(已知每千米耗油0.2升)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
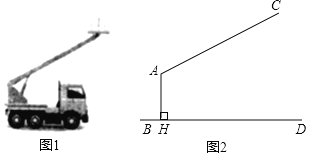
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:⊙O是正方形ABCD的外接圆,点E在![]() 上,连接BE、DE,点F在
上,连接BE、DE,点F在![]() 上连接BF、DF,BF与DE、DA分别交于点G、点H,且DA平分∠EDF.
上连接BF、DF,BF与DE、DA分别交于点G、点H,且DA平分∠EDF.
(1)如图1,求证:∠CBE=∠DHG;
(2)如图2,在线段AH上取一点N(点N不与点A、点H重合),连接BN交DE于点L,过点H作HK∥BN交DE于点K,过点E作EP⊥BN,垂足为点P,当BP=HF时,求证:BE=HK;
(3)如图3,在(2)的条件下,当3HF=2DF时,延长EP交⊙O于点R,连接BR,若△BER的面积与△DHK的面积的差为![]() ,求线段BR的长.
,求线段BR的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
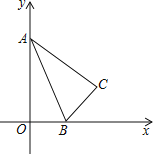
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束
的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束![]() 在这个运动过程中.
在这个运动过程中.
![]() 中点P经过的路径长______.
中点P经过的路径长______.
![]() 点C运动的路径长是______.
点C运动的路径长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
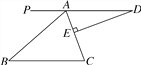
【题目】如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.
(1)求∠B的度数,并判断△ABC的形状;
(2)若延长线段DE恰好过点B,试说明DB是∠ABC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.
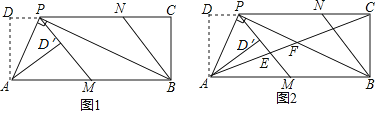
(1)求证:AD2=DPPC;
(2)请判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC,分别交PM,PB于点E,F.若![]() =
=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王在新藏公路某路段设置了一个加水站,他每天开着加水车沿东西方向给过路的汽车加水.如果约定向西为正.向东为负,加水车当天的行驶记录如下(单位:千米):
+8,-9,+7,-4,-3,+5,-6,-8,+6,+7.
(1)加水车最后到达的地方在出发点的哪个方向?距出发点多远?
(2)若加水车行驶过程中每千米耗油量为![]() 升,求这天加水车共耗油多少升?
升,求这天加水车共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com