
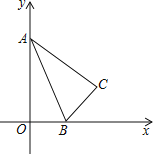
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束
的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束![]() 在这个运动过程中.
在这个运动过程中.
![]() 中点P经过的路径长______.
中点P经过的路径长______.
![]() 点C运动的路径长是______.
点C运动的路径长是______.
【答案】 ![]()
![]()
【解析】(1)根据直角三角形斜边中线等于斜边一半,确定中点P的运动路径:以O为圆心,以OP为半径的![]() 圆弧,半径OP=
圆弧,半径OP=![]() AB=2
AB=2![]() ,代入周长公式计算即可;
,代入周长公式计算即可;
(2)分为两种情况:
①当A从O到现在的点A处时,如图2,此时C′A⊥y轴,点C运动的路径长是CC′的长;
②当A再继续向上移动,直到点B与O重合时,如图3,此时点C运动的路径是从C′到C,长是CC′;
分别计算并相加.
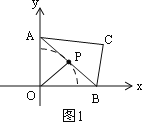
(1)如图1,∵∠AOB=90°,P为AB的中点,
∴OP=![]() AB,
AB,
∵AB=![]() ,
,
∴OP=2![]() ,
,
∴AB中点P运动的轨迹是以O为圆心,以OP为半径的![]() 圆弧,
圆弧,
即AB中点P经过的路径长=![]() ×2×2
×2×2![]() π=
π=![]() π;
π;
(2)①当A从O到现在的点A处时,如图2,此时C′A⊥y轴,
点C运动的路径长是CC′的长,
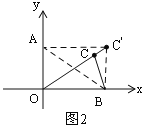
∴AC′=OC=8,
∵AC′∥OB,
∴∠AC′O=∠COB,
∴cos∠AC′O=cos∠COB=![]() ,
,
∴![]() ,
,
∴OC′=4![]() ,
,
∴CC′=4![]() -8;
-8;
②当A再继续向上移动,直到点B与O重合时,如图3,
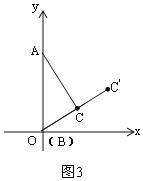
此时点C运动的路径是从C′到C,长是CC′,
CC′=OC′-BC=4![]() -4,
-4,
综上所述,点C运动的路径长是:4![]() -8+4
-8+4![]() -4=8
-4=8![]() -12;
-12;
故答案为:(1). ![]() (2).
(2). ![]()


科目:初中数学 来源: 题型:
【题目】如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的结论是( )
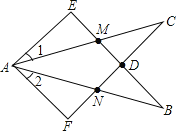
A.CD=DN;B.∠1=∠2;C.BE=CF;D.△ACN≌△ABM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电力公司为鼓励市民节约用电,采取按月用电量分段收费的办法,已知某户居民每月应缴电费y(元)与用电量x(度)的函数图象是一条折线(如图),根据图象解答下列问题.
(1)分别写出当0≤x≤100和x>100时,y与x间的函数关系式;
(2)若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元,则该用户该月用了多少度电?
查看答案和解析>>
科目:初中数学 来源: 题型:
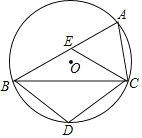
【题目】如图,△ABC是⊙O的内接三角形,点D在![]() 上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
(1)求证:AC=CE;
(2)求证:BC2﹣AC2=ABAC;
(3)已知⊙O的半径为3.
①若![]() =
=![]() ,求BC的长;
,求BC的长;
②当![]() 为何值时,ABAC的值最大?
为何值时,ABAC的值最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
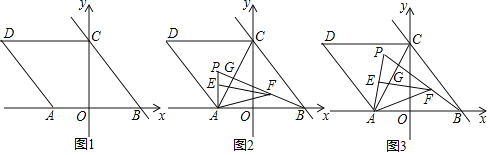
【题目】已知:在平面直角坐标系中,点O为坐标原点,点A在x轴的负半轴上,直线y=﹣![]() x+
x+![]() 与x轴、y轴分别交于B、C两点,四边形ABCD为菱形.
与x轴、y轴分别交于B、C两点,四边形ABCD为菱形.
(1)如图1,求点A的坐标;
(2)如图2,连接AC,点P为△ACD内一点,连接AP、BP,BP与AC交于点G,且∠APB=60°,点E在线段AP上,点F在线段BP上,且BF=AE,连接AF、EF,若∠AFE=30°,求AF2+EF2的值;
(3)如图3,在(2)的条件下,当PE=AE时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,b)、点B(a,0)、点D(d,0)且a、b、c满足![]() .DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
.DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
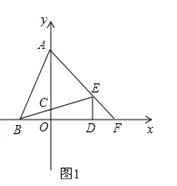
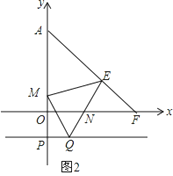
(1)求点A、B、D的坐标;
(2)求点C、E、F的坐标;
(3)如图,过P(0,-1)作x轴的平行线,在该平行线上有一点Q(点Q在P的右侧)使∠QEM=45°,QE交x轴于N,ME交y轴正半轴于M,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C为线段AB上一点,分别以AC、BC为边在线段AB的同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.
(1)如图1,若∠ACD=60°,则∠AFB=______,如图2,若∠ACD=90°,则∠AFB=______,如图3,若∠ACD=α,则∠AFB=______(用含α的式子表示);
(2)设∠ACD=α,将图3中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),如图4,试探究∠AFB与α的数量关系,并予以说明.
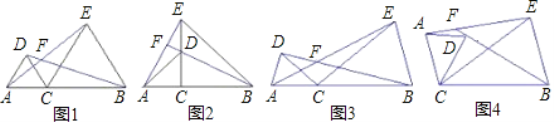
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把![]() 张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形的盒子底部,盒子底面未被覆盖的部分用阴影部分表示则图中两块阴影部分的周长的和是( )
张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形的盒子底部,盒子底面未被覆盖的部分用阴影部分表示则图中两块阴影部分的周长的和是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com