
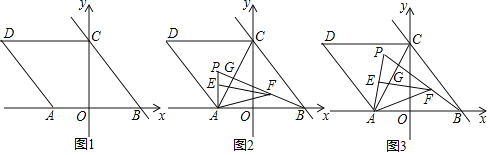
ЁОЬтФПЁПвбжЊЃКдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌЕуAдкxжсЕФИКАыжсЩЯЃЌжБЯпy=Љ![]() x+
x+![]() гыxжсЁЂyжсЗжБ№НЛгкBЁЂCСНЕуЃЌЫФБпаЮABCDЮЊСтаЮЃЎ
гыxжсЁЂyжсЗжБ№НЛгкBЁЂCСНЕуЃЌЫФБпаЮABCDЮЊСтаЮЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓЕуAЕФзјБъЃЛ
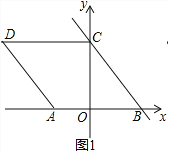
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгACЃЌЕуPЮЊЁїACDФквЛЕуЃЌСЌНгAPЁЂBPЃЌBPгыACНЛгкЕуGЃЌЧвЁЯAPB=60ЁуЃЌЕуEдкЯпЖЮAPЩЯЃЌЕуFдкЯпЖЮBPЩЯЃЌЧвBF=AEЃЌСЌНгAFЁЂEFЃЌШєЁЯAFE=30ЁуЃЌЧѓAF2+EF2ЕФжЕЃЛ
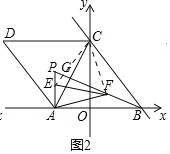
ЃЈ3ЃЉШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБPE=AEЪБЃЌЧѓЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉAЃЈЉ![]() ЃЌ0ЃЉЃЎЃЈ2ЃЉ49ЃЛЃЈ3ЃЉPЃЈЉ
ЃЌ0ЃЉЃЎЃЈ2ЃЉ49ЃЛЃЈ3ЃЉPЃЈЉ![]() ЃЌ3
ЃЌ3![]() ЃЉ
ЃЉ
ЁОНтЮіЁПЃЈ1ЃЉРћгУЙДЙЩЖЈРэЧѓГіBCЕФГЄМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉШчЭМ2жаЃЌСЌНгCEЁЂCFЃЎжЄУїЁїCEFЪЧЕШБпШ§НЧаЮЃЌAFЁЭCFМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉШчЭМ3жаЃЌбгГЄCEНЛFAЕФбгГЄЯпгкHЃЌзїPQЁЭABгкQЃЌPKЁЭOCгкKЃЌдкBPЩшНиШЁBT=PAЃЌСЌНгATЁЂCTЁЂCFЁЂPCЃЎжЄУїЁїAPFЪЧЕШБпШ§НЧаЮЃЌATЁЭPBМДПЩНтОіЮЪЬтЃЛ
ЃЈ1ЃЉШчЭМ1жаЃЌ
Ёпy=-Љ![]() x+
x+![]() ЃЌ
ЃЌ
ЁрBЃЈ![]() ЃЌ0ЃЉЃЌCЃЈ0ЃЌ
ЃЌ0ЃЉЃЌCЃЈ0ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрBO=![]() ЃЌOC=
ЃЌOC=![]() ЃЌ
ЃЌ
дкRtЁїOBCжаЃЌBC=![]() =7ЃЌ
=7ЃЌ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрAB=BC=7ЃЌ
ЁрOA=AB-OB=7-![]() =
=![]() ЃЌ
ЃЌ
ЁрAЃЈ-![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌСЌНгCEЁЂCFЃЎ
ЁпOA=OBЃЌCOЁЭABЃЌ
ЁрAC=BC=7ЃЌ
ЁрAB=BC=ACЃЌ
ЁрЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯACB=60ЁуЃЌ
ЁпЁЯAPB=60ЁуЃЌ
ЁрЁЯAPB=ЁЯACBЃЌ
ЁпЁЯPAG+ЁЯAPB=ЁЯAGB=ЁЯCBG+ЁЯACBЃЌ
ЁрЁЯPAG=ЁЯCBGЃЌЁпAE=BFЃЌ
ЁрЁїACEЁеЁїBCFЃЌ
ЁрCE=CFЃЌЁЯACE=ЁЯBCFЃЌ
ЁрЁЯECF=ЁЯACF+ЁЯACE=ЁЯACF+ЁЯBCF=ЁЯACB=60ЁуЃЌ
ЁрЁїCEFЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯCFE=60ЁуЃЌEF=FCЃЌ
ЁпЁЯAFE=30ЁуЃЌ
ЁрЁЯAFC=ЁЯAFE+ЁЯCFE=90ЁуЃЌ
дкRtЁїACFжаЃЌAF2+CF2=AC2=49ЃЌ
ЁрAF2+EF2=49ЃЎ
ЃЈ3ЃЉШчЭМ3жаЃЌбгГЄCEНЛFAЕФбгГЄЯпгкHЃЌзїPQЁЭABгкQЃЌPKЁЭOCгкKЃЌдкBPЩшНиШЁBT=PAЃЌСЌНгATЁЂCTЁЂCFЁЂPCЃЎ
ЁпЁїCEFЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯCEF=60ЁуЃЌEC=CFЃЌ
ЁпЁЯAFE=30ЁуЃЌЁЯCEF=ЁЯH+ЁЯEFHЃЌ
ЁрЁЯH=ЁЯCEF-ЁЯEFH=30ЁуЃЌ
ЁрЁЯH=ЁЯEFHЃЌ
ЁрEH=EFЃЌ
ЁрEC=EHЃЌ
ЁпPE=AEЃЌЁЯPEC=ЁЯAEHЃЌ
ЁрЁїCPEЁеЁїHAEЃЌ
ЁрЁЯPCE=ЁЯHЃЌ
ЁрPCЁЮFHЃЌ
ЁпЁЯCAP=ЁЯCBTЃЌAC=BCЃЌ
ЁрЁїACPЁеЁїBCTЃЌ
ЁрCP=CTЃЌЁЯACP=ЁЯBCTЃЌ
ЁрЁЯPCT=ЁЯACB=60ЁуЃЌ
ЁрЁїCPTЪЧЕШБпШ§НЧаЮЃЌ
ЁрCT=PTЃЌЁЯCPT=ЁЯCTP=60ЁуЃЌ
ЁпCPЁЮFHЃЌ
ЁрЁЯHFP=ЁЯCPT=60ЁуЃЌ
ЁпЁЯAPB=60ЁуЃЌ
ЁрЁїAPFЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯCFP=ЁЯAFC-ЁЯЁЯAFP=30ЁуЃЌ
ЁрЁЯTCF=ЁЯCTP-ЁЯTFC=30ЁуЃЌ
ЁрЁЯTCF=ЁЯTFCЃЌ
ЁрTF=TC=TPЃЌ
ЁрATЁЭPFЃЌЩш BF=mЃЌдђAE=PE=mЃЌ
ЁрPF=AP=2mЃЌTF=TP=mЃЌTB=2mЃЌBP=3mЃЌ
дкRtЁїAPTжаЃЌAT=![]() mЃЌ
mЃЌ
дкRtЁїABTжаЃЌЁпAT2+TB2=AB2ЃЌ
ЁрЃЈ![]() mЃЉ2+ЃЈ2mЃЉ2=72ЃЌ
mЃЉ2+ЃЈ2mЃЉ2=72ЃЌ
НтЕУm=![]() Лђ-
Лђ-![]() ЃЈЩсЦњЃЉЃЌ
ЃЈЩсЦњЃЉЃЌ
ЁрBF=![]() ЃЌAT=
ЃЌAT=![]() ЃЌBP=3
ЃЌBP=3![]() ЃЌsinЁЯABT=
ЃЌsinЁЯABT=![]() ЃЌ
ЃЌ
ЁпOK=PQ=BPsinЁЯPBQ=3![]() ЁС
ЁС![]() =3
=3![]() ЃЌBQ=
ЃЌBQ=![]() =6ЃЌ
=6ЃЌ
ЁрOQ=BQ-BO=6-![]() =
=![]() ЃЌ
ЃЌ
ЁрPЃЈ-![]() ЃЌ3
ЃЌ3![]() ЃЉ
ЃЉ


 ЗЂЩЂЫМЮЌаТПЮЬУЯЕСаД№АИ
ЗЂЩЂЫМЮЌаТПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtЁїCEFжаЃЌЁЯC=90ЁуЃЌЁЯCEF, ЁЯCFEЭтНЧЦНЗжЯпНЛгкЕуAЃЌЙ§ЕуAЗжБ№зїжБЯпCEЁЂCFЕФДЙЯпЃЌBЁЂDЮЊДЙзу.
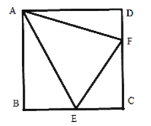
(1)ЧѓжЄ:ЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
(2)вбжЊABЕФГЄЮЊ6ЃЌЧѓ(BE+6)(DF+6)ЕФжЕЃЌ
(3)НшжњгкЩЯУцЮЪЬтЕФНтЬтЫМТЗЃЌНтОіЯТСаЮЪЬт:ШєШ§НЧаЮPQRжаЃЌЁЯQPR=45ЁуЃЌвЛЬѕИпЪЧPHЃЌГЄЖШЮЊ6,QH=2ЃЌдђHR= .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЁїABCжаЃЌAB=AC=12cmЃЌBC=9cmЃЌШєЕуQдкЯпЖЮCAЩЯвд4cm/sЕФЫйЖШгЩЕуCЯђЕуAдЫЖЏЃЌЕуPдкBCЯпЖЮЩЯвд3cm/sЕФЫйЖШгЩBЯђCдЫЖЏЃЌЧѓЖрГЄЪБМфЕуQгыЕуPЕквЛДЮдкФФЬѕБпЩЯЯргіЃПЃЈ ЃЉ
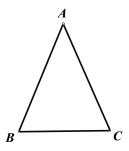
A.24s BCБпB.12s BCБп
C.24s ABБпD.12s ACБп
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌИпADКЭBEЫљдкЕФжБЯпНЛгкЕуHЃЌЧвBHЃНACЃЌдђЁЯABCЕШгк(ЁЁ)
A. 45Ёу B. 120Ёу C. 45ЁуЛђ135Ёу D. 45ЁуЛђ120Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
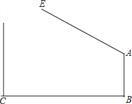
ЁОЬтФПЁПвбжЊЃКдкЫФБпаЮABCDжаЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуEЃЌЧвACЁЭBDЃЌзїBFЁЭCDЃЌДЙзуЮЊЕуFЃЌBFгыACНЛгкЕуCЃЌЁЯBGE=ЁЯADEЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКAD=CDЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌBHЪЧЁїABEЕФжаЯпЃЌШєAE=2DEЃЌDE=EGЃЌдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГіЭМ2жаЫФИіШ§НЧаЮЃЌЪЙаДГіЕФУПИіШ§НЧаЮЕФУцЛ§ЖМЕШгкЁїADEУцЛ§ЕФ2БЖЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФаББпдкxжсЕФе§АыжсЩЯЃЌЕуAгыдЕужиКЯЃЌЫцзХЖЅЕуAгЩOЕуГіЗЂбиyжсЕФе§АыжсЗНЯђЛЌЖЏЃЌЕуBвВбизХxжсЯђЕуOЛЌЖЏЃЌжБЕНгыЕуOжиКЯЪБдЫЖЏНсЪј
ЕФаББпдкxжсЕФе§АыжсЩЯЃЌЕуAгыдЕужиКЯЃЌЫцзХЖЅЕуAгЩOЕуГіЗЂбиyжсЕФе§АыжсЗНЯђЛЌЖЏЃЌЕуBвВбизХxжсЯђЕуOЛЌЖЏЃЌжБЕНгыЕуOжиКЯЪБдЫЖЏНсЪј![]() дкетИідЫЖЏЙ§ГЬжаЃЎ
дкетИідЫЖЏЙ§ГЬжаЃЎ
![]() жаЕуPОЙ§ЕФТЗОЖГЄ______ЃЎ
жаЕуPОЙ§ЕФТЗОЖГЄ______ЃЎ
![]() ЕуCдЫЖЏЕФТЗОЖГЄЪЧ______ЃЎ
ЕуCдЫЖЏЕФТЗОЖГЄЪЧ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAЕФзјБъЮЊЃЈ4ЃЌ2ЃЉЃЎНЋЕуAШЦзјБъдЕуOа§зЊ90ЁуКѓЃЌдйЯђзѓЦНвЦ1ИіЕЅЮЛГЄЖШЕУЕНЕуAЁфЃЌдђЙ§ЕуAЁфЕФе§БШР§КЏЪ§ЕФНтЮіЪНЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
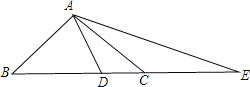
ЁОЬтФПЁП(1)ШчЭМЃЌдкдкЁїABCжаЃЌвбжЊЁЯBAC=900ЃЌAB=AC,ЕуDдкBCЩЯЃЌЧвBD=BAЃЌЕуEдкBCЕФбгГЄЯпЩЯЃЌCE=CAЃЌЧѓЁЯDAEЕФЖШЪ§ЃЛ
(2)ШчЙћАбЃЈ1ЃЉжаЕФЁАAB=ACЁБЬѕМўШЅЕєЃЌЦфгрЬѕМўВЛБфЃЌФЧУДЁЯDAEЕФЖШЪ§ИФБфТ№ЃПЮЊЪВУДЃП
(3)ШчЙћАбЃЈ1ЃЉжаЕФЁАЁЯBAC=900ЁБИФГЩЁАЁЯBAC>900ЁБЦфгрЬѕМўВЛБфЃЌЪдЬНОПЁЯDAEгыЁЯBACЕФЪ§СПЙиЯЕЪНЃЌЪджЄУї.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌбЇаЃДѓУХГіПкДІгавЛздЖЏИагІРИИЫЃЌЕуAЪЧРИИЫзЊЖЏЕФжЇЕуЃЌЕБГЕСООЙ§ЪБЃЌРИИЫAEЛсздЖЏЩ§Ц№ЃЌФГЬьдчЩЯЃЌРИИЫЗЂЩњЙЪеЯЃЌдкФГИіЮЛжУЭЛШЛПЈзЁЃЌетЪБВтЕУРИИЫЩ§Ц№ЕФНЧЖШЁЯBAE=127ЁуЃЌвбжЊABЁЭBCЃЌжЇМмABИп1.2УзЃЌДѓУХДђПЊЕФПэЖШBCЮЊ2УзЃЌвдЯТФФСОГЕПЩвдЭЈЙ§ЃПЃЈРИИЫПэЖШЃЌЦћГЕЗДЙтОЕКіТдВЛМЦЃЉЃЈВЮПМЪ§ОнЃКsin37ЁуЁж0.60ЃЌcos37ЁуЁж0.80ЃЌtan37ЁуЁж0.75ЃЎГЕСОГпДчЃКГЄЁСПэЁСИпЃЉЃЈЁЁЁЁЃЉ
A. БІТэZ4ЃЈ4200mmЁС1800mmЁС1360mmЃЉ B. БМГлsmartЃЈ4000mmЁС1600mmЁС1520mmЃЉ
C. ДѓжкРЪвнЃЈ4600mmЁС1700mmЁС1400mmЃЉ D. АТЕЯA6LЃЈ4700mmЁС1800mmЁС1400mmЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com