
【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门打开的宽度BC为2米,以下哪辆车可以通过?(栏杆宽度,汽车反光镜忽略不计)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)( )
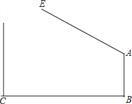
A. 宝马Z4(4200mm×1800mm×1360mm) B. 奔驰smart(4000mm×1600mm×1520mm)
C. 大众朗逸(4600mm×1700mm×1400mm) D. 奥迪A6L(4700mm×1800mm×1400mm)
【答案】C
【解析】试题解析:如图,过点A作BC的平行线AG,过点N作NQ⊥BC于Q,交AG于点R,
则∠BAG=90°,
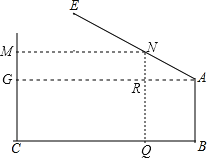
∵∠BAE=127°,∠BAG=90°,
∴∠EAH=∠EAB-∠BAG=37°.
在△NAR中,∠ARN=90°,∠EAG=37°,
当车宽为1.8m,则GR=1.8m,故AR=2-1.8=0.2(m),
∴NR=ARtan37°=0.2×0.75=0.15(m),
∴NQ=1.2+0.15=1.35<1.36,
∴宝马Z4(4200mm×1800mm×1360mm)无法通过,
∴奥迪A4(4700mm×1800mm×1400mm)无法通过,
故此选项A,D不合题意;
当车宽为1.6m,则GR=1.6m,故AR=2-1.6=0.4(m),
∴NR=ARtan37°=0.4×0.75=0.3(m),
∴NQ=1.2+0.3=1.5<1.52,
∴奇瑞QQ(4000mm×1600mm×1520mm)无法通过,故此选项不合题意;
当车宽为1.7m,则GR=1.7m,故AR=2-1.7=0.3(m),
∴NR=ARtan37°=0.3×0.75=0.225(m),
∴NQ=1.2+0.225=1.425>1.4,
∴大众朗逸(4600mm×1700mm×1400mm)可以通过,故此选项符合题意;
故选C.


科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点O为坐标原点,点A在x轴的负半轴上,直线y=﹣![]() x+
x+![]() 与x轴、y轴分别交于B、C两点,四边形ABCD为菱形.
与x轴、y轴分别交于B、C两点,四边形ABCD为菱形.
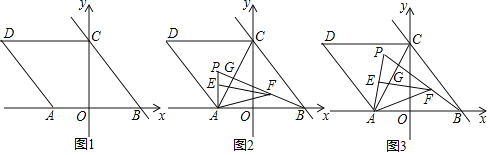
(1)如图1,求点A的坐标;
(2)如图2,连接AC,点P为△ACD内一点,连接AP、BP,BP与AC交于点G,且∠APB=60°,点E在线段AP上,点F在线段BP上,且BF=AE,连接AF、EF,若∠AFE=30°,求AF2+EF2的值;
(3)如图3,在(2)的条件下,当PE=AE时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织学生乘汽车去自然保护区野营,先以60km/h的速度走平路,后又以30km/h的速度爬坡,共用了6.5h;原路返回时,汽车以40km/h的速度下坡,又以50km/h的速度走平路,共用了6 h。问平路和坡路各有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某超市分别以每盏150元,190元的进价购进A,B两种品牌的护眼灯,下表是近两天的销售情况.
销售日期 | 销售数量(盏) | 销售收入(元) | |
A品牌 | B品牌 | ||
第一天 | 2 | 1 | 680 |
第二天 | 3 | 4 | 1670 |
(1)求A,B两种品牌护眼灯的销售价;
(2)若超市准备用不超过4900元的金额购进这两种品牌的护眼灯共30盏,求B品牌的护眼灯最多采购多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 [问题解决]:如图1,已知AB∥CD,E是直线AB,CD内部一点,连接BE,DE,若∠ABE=40°,∠CDE=60°,求∠BED的度数.
嘉琪想到了如图2所示的方法,但是没有解答完,下面是嘉淇未完成的解答过程:
解:过点E作EF∥AB,
∴∠ABE=∠BEF=40°
∵AB∥CD,
∴EF∥CD,
…
请你补充完成嘉淇的解答过程:
[问题迁移]:请你参考嘉琪的解题思路,完成下面的问题:
如图3,AB∥CD,射线OM与直线AB,CD分别交于点A,C,射线ON与直线AB,CD分别交于点B,D,点P在射线ON上运动,设∠BAP=α,∠DCP=β.
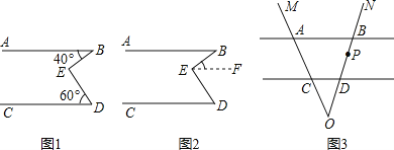
(1)当点P在B,D两点之间运动时(P不与B,D重合),求α,β和∠APC之间满足的数量关系.
(2)当点P在B,D两点外侧运动时(P不与点O重合),直接写出α,β和∠APC之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把![]() 张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形的盒子底部,盒子底面未被覆盖的部分用阴影部分表示则图中两块阴影部分的周长的和是( )
张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形的盒子底部,盒子底面未被覆盖的部分用阴影部分表示则图中两块阴影部分的周长的和是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
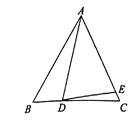
【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE ,设∠BAD=α,∠CDE=β.
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°, 那么α=_______,β=_______.
②求α、β之间的关系式.
(2)是否存在不同于以上②中的α、β之间的关系式?若存在,求出这个关系式,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中AD是∠A的外角平分线,P是AD上一动点且不与点A、D重合,记PB+PC=a,AB+AC=b,则a、b的大小关系是( )
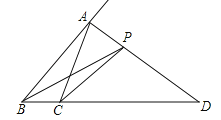
A.a>b B.a=b C.a<b D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
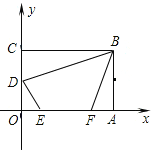
【题目】在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=3.当四边形BDEF的周长最小时,点E的坐标是( )
A. (![]() ,0) B. (1,0) C. (
,0) B. (1,0) C. (![]() ,0) D. (2,0)
,0) D. (2,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com