练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

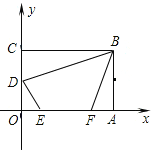
    【题目】在平面直角坐标系中，矩形OABC如图所示．点A在x轴正半轴上，点C在y轴正半轴上，且OA=6，OC=4，D为OC中点，点E、F在线段OA上，点E在点F左侧，EF=3．当四边形BDEF的周长最小时，点E的坐标是（　　）

    A. （ ，0） B. （1，0） C. (，0) D. （2，0）

    【答案】B

    【解析】

    以D、E、F为顶点作平行四边形DEF,作出点B关于x轴对称点B',则易得到B'的坐标,D'的坐标,然后利用待定系数法求出直线的解析式,令y=0,确定F点坐标,也即可得到E点坐标.
    详解:以D、E、F为顶点作平行四边形DEF,作出点B关于x轴对称点B',如图,

    ∵B(6,4),
    ∴ 的坐标为(6,4),
    D=EF=3,D(0,2),
    ∴的坐标为(3,2),
    设直线的解析式为y=kx+b,
    把(6,-4), (3,2)代入得,
    ,
    解得k=-2,b=8,
    ∴直线的解析式为y=-2x+8,
    令y=0,得-2x+8=0,解得x=4,
    ∴F(4,0),E(1,0).故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

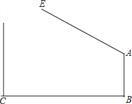
    【题目】如图，学校大门出口处有一自动感应栏杆，点A是栏杆转动的支点，当车辆经过时，栏杆AE会自动升起，某天早上，栏杆发生故障，在某个位置突然卡住，这时测得栏杆升起的角度∠BAE=127°，已知AB⊥BC，支架AB高1.2米，大门打开的宽度BC为2米，以下哪辆车可以通过？（栏杆宽度，汽车反光镜忽略不计）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75．车辆尺寸：长×宽×高）（　　）

    A. 宝马Z4（4200mm×1800mm×1360mm） B. 奔驰smart（4000mm×1600mm×1520mm）

    C. 大众朗逸（4600mm×1700mm×1400mm） D. 奥迪A6L（4700mm×1800mm×1400mm）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简，再求值：

    （1）2m2－4m＋1－2（m2＋2m－），其中m＝－1；

    （2）5xy2－[2x2y－（2x2y－3xy2）]，其中（x－2）2＋|y＋1|＝0.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC=10，sinB=，

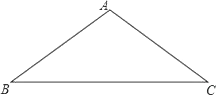
    （1）求边BC的长；

    （2）将△ABC绕着点C旋转得△A′B′C，点A的对应点A′，点B的对应点B′．如果点A′在BC边上，那么点B和点B′之间的距离等于多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，C是线段AB的中点，CD平分∠ACE，CE平分∠BCD，CD=CE．

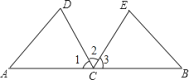
    (1)求证：△ACD≌△BCE；

    (2)若∠D=75°，求∠B的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图是一个长为，宽为的长方形，沿图中虚线剪开分成四块小长方形，然后按图的形状拼成一个正方形．（）

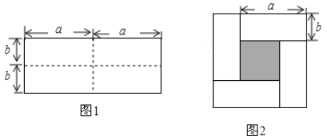
    （1）图2的阴影部分的正方形的边长是____．

    （2）用两种不同的方法求图中阴影部分的面积．

    （方法）阴影＝____________________；

    （方法）阴影＝____________________；

    （3）利用（方法）（方法）中两个代数式之间存在的等量关系，解决问题：若，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

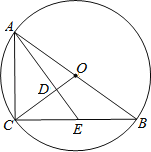
    【题目】如图，⊙O是Rt△ABC的外接圆，∠ACB=90°，E为BC上一点，连接AE与OC交于点D，∠CAE=∠CBA．

    （1）求证：AE⊥OC；

    （2）若⊙O的半径为5，AE的长为6，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为创建全国文明城市，开展“美化绿化城市”活动，计划经过若干年使城区绿化总面积新增360万平方米．自2013年初开始实施后，实际每年绿化面积是原计划的1.5倍，这样可提前4年完成任务．

    (1)问实际每年绿化面积多少万平方米？

    (2)为加大创城力度，市政府决定从2017年起加快绿化速度，要求不超过2年完成，那么实际平均每年绿化面积至少还要增加多少万平方米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线l：y=﹣x2+bx+c（b，c为常数），其顶点E在正方形ABCD内或边上，已知点A（1，2），B（1，1），C（2，1）．

    （1）直接写出点D的坐标_____________；

    （2）若l经过点B，C，求l的解析式；

    （3）设l与x轴交于点M，N，当l的顶点E与点D重合时，求线段MN的值；当顶点E在正方形ABCD内或边上时，直接写出线段MN的取值范围；

    （4）若l经过正方形ABCD的两个顶点，直接写出所有符合条件的c的值．

    查看答案和解析>>

    同步练习册答案