
【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
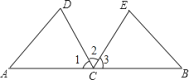
(1)求证:△ACD≌△BCE;
(2)若∠D=75°,求∠B的度数.
【答案】(1)详见解析;(2)45°.
【解析】
(1)先利用角平分线性质、以及等量代换,可证出∠1=∠3,结合CD=CE,C是AB中点,即AC=BC,利用SAS可证全等;
(2)利用角平分线性质,可知∠1=∠2,∠2=∠3,从而求出∠1=∠2=∠3,再利用全等三角形的性质可得出∠E=∠D,在△BCE中,利用三角形内角和是180°,可求出∠B.
(1)证明:∵点C是线段AB的中点,
∴AC=BC,
又∵CD平分∠ACE,CE平分∠BCD,
∴∠1=∠2,∠2=∠3,
∴∠1=∠3,
∵在△ACD和△BCE中,
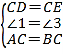 ,
,
∴△ACD≌△BCE(SAS).
(2)∵∠1+∠2+∠3=180°,
∴∠1=∠2=∠3=60°,
∵△ACD≌△BCE,
∴∠E=∠D=75°,
∴∠B=180°-∠E-∠3=180°-75°-60°=45°.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】 [问题解决]:如图1,已知AB∥CD,E是直线AB,CD内部一点,连接BE,DE,若∠ABE=40°,∠CDE=60°,求∠BED的度数.
嘉琪想到了如图2所示的方法,但是没有解答完,下面是嘉淇未完成的解答过程:
解:过点E作EF∥AB,
∴∠ABE=∠BEF=40°
∵AB∥CD,
∴EF∥CD,
…
请你补充完成嘉淇的解答过程:
[问题迁移]:请你参考嘉琪的解题思路,完成下面的问题:
如图3,AB∥CD,射线OM与直线AB,CD分别交于点A,C,射线ON与直线AB,CD分别交于点B,D,点P在射线ON上运动,设∠BAP=α,∠DCP=β.
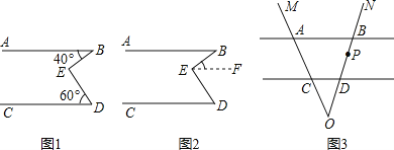
(1)当点P在B,D两点之间运动时(P不与B,D重合),求α,β和∠APC之间满足的数量关系.
(2)当点P在B,D两点外侧运动时(P不与点O重合),直接写出α,β和∠APC之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种夹克和T恤,夹克每件定价180元,T恤每件定价60元,厂家在开展促销活动期间,向顾客提供了两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的80%付款;现在某客户要到该厂购买夹克30件,T恤![]() 件(
件(![]() >
>![]() ).
).
(1)若该客户按方案①购买付款 元(用含![]() 的式子表示);若该客户按方案②购买付款 元(用含
的式子表示);若该客户按方案②购买付款 元(用含![]() 的式子表示).
的式子表示).
(2)当![]() 时,通过计算说明方案①、方案②哪种方案购买较为合算?
时,通过计算说明方案①、方案②哪种方案购买较为合算?
(3)当![]() 时,你能给出更为省钱的购买方案吗?试写出你的购买方法.
时,你能给出更为省钱的购买方案吗?试写出你的购买方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学的高中部在A校区,初中部在B校区,学校学生会计划在3月12日植树节当天安排部分学生到郊区公园参加植树活动.已知A校区的每位高中学生往返车费是6元,B校区的每位初中学生往返的车费是10元,要求初、高中均有学生参加,且参加活动的初中学生比参加活动的高中学生多4人,本次活动的往返车费总和不超过210元,求初、高中最多各有多少学生参加.
查看答案和解析>>
科目:初中数学 来源: 题型:
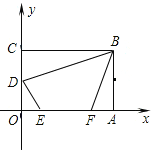
【题目】在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=3.当四边形BDEF的周长最小时,点E的坐标是( )
A. (![]() ,0) B. (1,0) C. (
,0) B. (1,0) C. (![]() ,0) D. (2,0)
,0) D. (2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
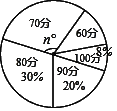
【题目】某班共50名同学,统一参加区教育局举办的防“雾霾”知识检验,成绩分别记作60分、70分、80分、90分、100分,现统计出80分、90分、100分的人数,制成不完整的扇形统计图.
(1)若n=108,则60分的人数为 ;
(2)若从这50份试卷中,随机抽取一份,求抽到试卷的分数低于80分的概率;
(3)若成绩的唯一众数为80分,求这个班平均成绩的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com