
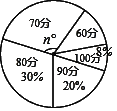
【题目】某班共50名同学,统一参加区教育局举办的防“雾霾”知识检验,成绩分别记作60分、70分、80分、90分、100分,现统计出80分、90分、100分的人数,制成不完整的扇形统计图.
(1)若n=108,则60分的人数为 ;
(2)若从这50份试卷中,随机抽取一份,求抽到试卷的分数低于80分的概率;
(3)若成绩的唯一众数为80分,求这个班平均成绩的最大值.
【答案】(1) 6人;(2) ![]() (3) 78
(3) 78
【解析】(1)、根据n的值得出70分所占的百分比,从而得出60分所占的百分比,从而得出人数;(2)、首先求出低于80分的人数,然后根据概率的计算法则得出答案;(3)、根据题意可得80分的人数为15人,根据80为唯一的众数可知70分的人数为14人时,这个班的平均数最大,从而根据平均数的求法得出答案.
(1)、若n=108, 则![]() ×100%=30%,
×100%=30%,
∴60分的学生所占比例为:1﹣30%﹣30%﹣20%﹣8%=12%,则60分的人数为:12%×50=6(人);
(2)、低于80分的人数为:50×(12%+30%)=21(人),
则从这50份试卷中,随机抽取一份,求抽到试卷的分数低于80分的概率为:![]() ;
;
(3)、∵80分的人数为:50×30%=15(人),且80分为成绩的唯一众数,所以当70分的人数为14人时,这个班的平均数最大,
∴最大值为:(50×8%×100+50×20%×90+50×30%×80+14×70+7×60)÷50=78(分).


科目:初中数学 来源: 题型:
【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
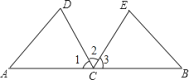
(1)求证:△ACD≌△BCE;
(2)若∠D=75°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
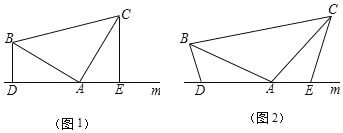
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,证明:△ABD≌△ACE,DE=BD+CE;
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D, A, E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,经过原点O的抛物线y=ax2+bx(a、b为常数,a≠0)与x轴相交于另一点A(3,0).直线l:y=x在第一象限内和此抛物线相交于点B(5,t),与抛物线的对称轴相交于点C.
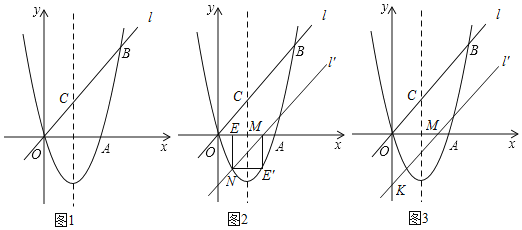
(1)求抛物线的解析式;
(2)在x轴上找一点P,使以点P、O、C为顶点的三角形与以点A、O、B为顶点的三角形相似,求满足条件的点P的坐标;
(3)直线l沿着x轴向右平移得到直线l′,l′与线段OA相交于点M,与x轴下方的抛物线相交于点N,过点N作NE⊥x轴于点E.把△MEN沿直线l′折叠,当点E恰好落在抛物线上时(图2),求直线l′的解析式;
(4)在(3)问的条件下(图3),直线l′与y轴相交于点K,把△MOK绕点O顺时针旋转90°得到△M′OK′,点F为直线l′上的动点.当△M'FK′为等腰三角形时,求满足条件的点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
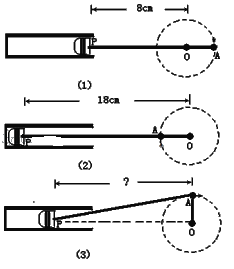
【题目】如图,曲柄连杆装置是很多机械上不可缺少的,曲柄OA绕O点圆周运动,连杆AP拉动活塞作往复运动.当曲柄的A旋转到最右边时,如图(1),OP长为8cm;当曲柄的A旋转到最左边时,如图(2)OP长为18cm.
(1)求曲柄OA和连杆AP分别有多长;
(2)求:OA⊥OP时,如图(3),OP的长是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线l:y=﹣x2+bx+c(b,c为常数),其顶点E在正方形ABCD内或边上,已知点A(1,2),B(1,1),C(2,1).
(1)直接写出点D的坐标_____________;
(2)若l经过点B,C,求l的解析式;
(3)设l与x轴交于点M,N,当l的顶点E与点D重合时,求线段MN的值;当顶点E在正方形ABCD内或边上时,直接写出线段MN的取值范围;
(4)若l经过正方形ABCD的两个顶点,直接写出所有符合条件的c的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
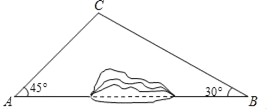
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
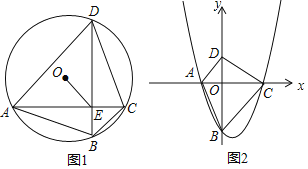
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有 ;
②在凸四边形ABCD中,AB=AD且CB≠CD,则该四边形 “十字形”.(填“是”或“不是”)
(2)如图1,A,B,C,D是半径为1的⊙O上按逆时针方向排列的四个动点,AC与BD交于点E,∠ADB﹣∠CDB=∠ABD﹣∠CBD,当6≤AC2+BD2≤7时,求OE的取值范围;
(3)如图2,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a,b,c为常数,a>0,c<0)与x轴交于A,C两点(点A在点C的左侧),B是抛物线与y轴的交点,点D的坐标为(0,﹣ac),记“十字形”ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为S1,S2,S3,S4.求同时满足下列三个条件的抛物线的解析式;
①![]() =
=![]()
![]() ;②
;②![]()
![]() =
=![]()
![]() ;③“十字形”ABCD的周长为12
;③“十字形”ABCD的周长为12![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
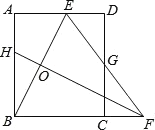
【题目】如图,矩形ABCD中,AB=8,点E是AD上的一点,有AE=4,BE的垂直平分线交BC的延长线于点F,连结EF交CD于点G.若G是CD的中点,则BC的长是___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com