
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有 ;
②在凸四边形ABCD中,AB=AD且CB≠CD,则该四边形 “十字形”.(填“是”或“不是”)
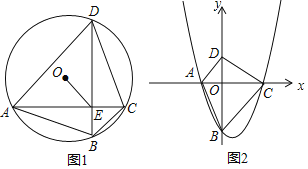
(2)如图1,A,B,C,D是半径为1的⊙O上按逆时针方向排列的四个动点,AC与BD交于点E,∠ADB﹣∠CDB=∠ABD﹣∠CBD,当6≤AC2+BD2≤7时,求OE的取值范围;
(3)如图2,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a,b,c为常数,a>0,c<0)与x轴交于A,C两点(点A在点C的左侧),B是抛物线与y轴的交点,点D的坐标为(0,﹣ac),记“十字形”ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为S1,S2,S3,S4.求同时满足下列三个条件的抛物线的解析式;
①![]() =
=![]()
![]() ;②
;②![]()
![]() =
=![]()
![]() ;③“十字形”ABCD的周长为12
;③“十字形”ABCD的周长为12![]() .
.
【答案】(1)①菱形,正方形;②不是;(2)![]() (OE>0);(3)y=x2﹣9.
(OE>0);(3)y=x2﹣9.
【解析】(1)利用“十字形”的定义判断即可;
(2)先判断出∠ADB+∠CAD=∠ABD+∠CAB,进而判断出∠AED=∠AEB=90°,即:AC⊥BD,再判断出四边形OMEN是矩形,进而得出OE2=2-![]() (AC2+BD2),即可得出结论;
(AC2+BD2),即可得出结论;
(3)由题意得,A(![]() ,0),B(0,c),C(
,0),B(0,c),C(![]() ,0),D(0,-ac),求出S=
,0),D(0,-ac),求出S=![]() ACBD=-
ACBD=-![]() (ac+c)×
(ac+c)×![]() ,S1=
,S1=![]() OAOB=-
OAOB=-![]() ,S2=
,S2=![]() OCOD=-
OCOD=-![]() ,S3=
,S3=![]() OA×OD=-
OA×OD=-![]() ,S4=
,S4=![]() OB×OC=-
OB×OC=-![]() ,进而建立方程
,进而建立方程![]() ,求出a=1,再求出b=0,进而判断出四边形ABCD是菱形,求出AD=3
,求出a=1,再求出b=0,进而判断出四边形ABCD是菱形,求出AD=3![]() ,进而求出c=-9,即可得出结论.
,进而求出c=-9,即可得出结论.
(1)①∵菱形,正方形的对角线互相垂直,
∴菱形,正方形是:“十字形”,
∵平行四边形,矩形的对角线不一定垂直,
∴平行四边形,矩形不是“十字形”,
故答案为:菱形,正方形;
②如图,
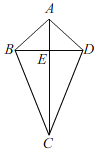
当CB=CD时,在△ABC和△ADC中,
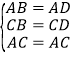 ,
,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
∵AB=AD,
∴AC⊥BD,
∴当CB≠CD时,四边形ABCD不是“十字形”,
故答案为:不是;
(2)∵∠ADB+∠CBD=∠ABD+∠CDB,∠CBD=∠CDB=∠CAB,
∴∠ADB+∠CAD=∠ABD+∠CAB,
∴180°﹣∠AED=180°﹣∠AEB,
∴AC⊥BD,
过点O作OM⊥AC于M,ON⊥BD于N,连接OA,OD,
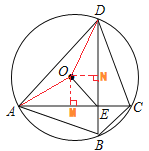
∴OA=OD=1,OM2=OA2﹣AM2,ON2=OD2﹣DN2,AM=![]() AC,DN=
AC,DN=![]() BD,四边形OMEN是矩形,
BD,四边形OMEN是矩形,
∴ON=ME,OE2=OM2+ME2,
∴OE2=OM2+ON2=2﹣![]() (AC2+BD2),
(AC2+BD2),
∵6≤AC2+BD2≤7,
∴2﹣![]() ≤OE2≤2﹣
≤OE2≤2﹣![]() ,
,
∴![]() ≤OE2≤
≤OE2≤![]() ,
,
∴![]() ≤OE≤
≤OE≤![]() ;
;
(3)由题意得,A(![]() ,0),B(0,c),C(
,0),B(0,c),C(![]() ,0),D(0,﹣ac),
,0),D(0,﹣ac),
∵a>0,c<0,
∴OA=![]() ,OB=﹣c,OC=
,OB=﹣c,OC=![]() ,OD=﹣ac,AC=
,OD=﹣ac,AC=![]() ,BD=﹣ac﹣c,
,BD=﹣ac﹣c,
∴S=![]() ACBD=﹣
ACBD=﹣![]() (ac+c)×
(ac+c)×![]() ,S1=
,S1=![]() OAOB=﹣
OAOB=﹣![]() ,S2=
,S2=![]() OCOD=﹣
OCOD=﹣![]() ,
,
S3=![]() OA×OD=﹣
OA×OD=﹣![]() ,S4=
,S4=![]() OB×OC=﹣
OB×OC=﹣![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() =2,
=2,
∴a=1,
∴S=﹣c![]() ,S1=﹣
,S1=﹣![]() ,S4=﹣
,S4=﹣![]() ,
,
∵![]() ,
,
∴S=S1+S2+2![]() ,
,
∴﹣c![]() =﹣
=﹣![]() ,
,
∴![]()
∴![]()
∴b=0,
∴A(![]() ,0),B(0,c),C(
,0),B(0,c),C(![]() ,0),d(0,﹣c),
,0),d(0,﹣c),
∴四边形ABCD是菱形,
∴4AD=12![]() ,
,
∴AD=3![]() ,
,
即:AD2=90,
∵AD2=c2﹣c,
∴c2﹣c=90,
∴c=﹣9或c=10(舍),
即:y=x2﹣9.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
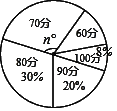
【题目】某班共50名同学,统一参加区教育局举办的防“雾霾”知识检验,成绩分别记作60分、70分、80分、90分、100分,现统计出80分、90分、100分的人数,制成不完整的扇形统计图.
(1)若n=108,则60分的人数为 ;
(2)若从这50份试卷中,随机抽取一份,求抽到试卷的分数低于80分的概率;
(3)若成绩的唯一众数为80分,求这个班平均成绩的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
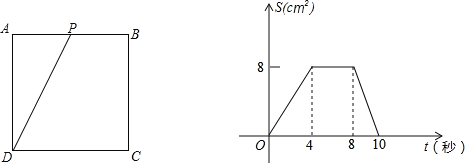
【题目】如图,正方形ABCD的边长为4cm,动点P从A点出发,在正方形的边上沿A→B→C→D运动,设运动的时间为t(s),△APD的面积为S(cm2),S与t的函数图象如图所示,请回答下列问题:
(1)点P在AB上运动时间为 s,在CD上运动的速度为 cm/s,△APD的面积S的最大值为 cm2;
(2)将S与t之间的函数关系式补充完整S=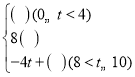 ;
;
(3)请求出运动时间t为几秒时,△APD的面积为6cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CDE=55°.如图,则∠EAB的度数为_________
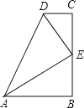
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AB=CB, BD=BE, ∠ABC=∠DBE=α.



(1)当α=60°, 如图则,∠DPE的度数______________
(2)若△BDE绕点B旋转一定角度,如图所示,求∠DPE(用α表示)
(3)当α=90°,其他条件不变,F为AD的中点,求证 :EC ⊥ BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,高BD、CE相交于点O,连接AO并延长交BC于点F,则图中全等的直角三角形共有( )

A. 4对B. 5对C. 6对D. 7对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,试解决下列问题:
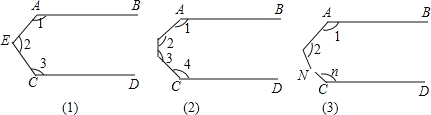
(1)图(1)中,∠1+∠2+∠3= ;
(2)图(2)中,∠1+∠2+∠3+∠4= ;
(3)图(3)中,∠1+∠2+∠3+…+∠n= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com