
【题目】如图, AB=CB, BD=BE, ∠ABC=∠DBE=α.



(1)当α=60°, 如图则,∠DPE的度数______________
(2)若△BDE绕点B旋转一定角度,如图所示,求∠DPE(用α表示)
(3)当α=90°,其他条件不变,F为AD的中点,求证 :EC ⊥ BF
【答案】(1)60°;(2)α;(3)证明见解析.
【解析】
(1)由SAS证明△ABE≌△CBD,得到∠AEB=∠CDB,再由对顶角相等及三角形内角和公式可得∠EPD=∠EBD即可;
(2)与(1)同理可求∠DPE=∠DBE,即可得出结论;
(3)延长BF到K,使FK=BF,连接KD,延长EC交BK于M.由SAS证明△AFB≌△DFK,得到AB=KD,∠ABF=∠DKF,进而得到BC=KD,KD∥AB,再证明∠BDK=∠4,得到△EBC≌△BDK,由全等三角形对应角相等得到∠1=∠2,即可得出结论.
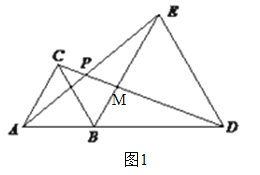
(1)如图1,设BE和CD相交于M.
∵∠ABC=∠DBE,∴∠ABE=∠CBD.
在△ABE和△CBD中,∵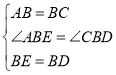 ,∴△ABE≌△CBD(SAS),∴∠AEB=∠CDB.
,∴△ABE≌△CBD(SAS),∴∠AEB=∠CDB.
在△PME和△BMD中,∵∠PME=∠BMD,∠AEB=∠CDB,∴∠EPD=180°-∠AEB-∠PME=180°-∠CDB-∠BMD=∠MBD=60°;
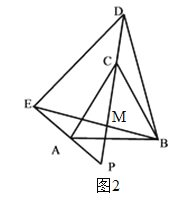
(2)如图2,同理可求∠DPE=∠DBE=α;
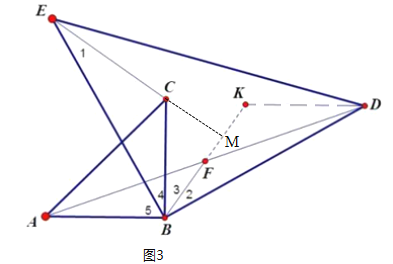
(3)如图3,延长BF到K,使FK=BF,连接KD,延长EC交BK于M.
∵AF=DF,∠AFB=∠DFK,BF=KF,∴△AFB≌△DFK,∴AB=KD,∠ABF=∠DKF,∴BC=KD,KD∥AB,∴∠BDK+∠ABD=180°,∴∠BDK=180°-∠ABD=180°-(∠2+∠3+∠4+∠5)=180°-[(90°-∠4)+90°]=∠4.
在△EBC和△BDK中,∵EB=BD,∠4=∠BDK,BC=DK,∴△EBC≌△BDK,∴∠1=∠2.
∵∠2+∠EBK=90°,∴∠1+∠EBK=90°,∴∠EMB=90°,∴EC⊥BF.


科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.5倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2017年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线l:y=﹣x2+bx+c(b,c为常数),其顶点E在正方形ABCD内或边上,已知点A(1,2),B(1,1),C(2,1).
(1)直接写出点D的坐标_____________;
(2)若l经过点B,C,求l的解析式;
(3)设l与x轴交于点M,N,当l的顶点E与点D重合时,求线段MN的值;当顶点E在正方形ABCD内或边上时,直接写出线段MN的取值范围;
(4)若l经过正方形ABCD的两个顶点,直接写出所有符合条件的c的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
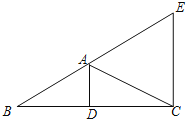
【题目】如图,在△ABC中,AD是边BC上的中线,∠BAD=∠CAD,CE∥AD,CE交BA的延长线于点E,BC=8,AD=3.
(1)求CE的长;
(2)求证:△ABC为等腰三角形.
(3)求△ABC的外接圆圆心P与内切圆圆心Q之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有 ;
②在凸四边形ABCD中,AB=AD且CB≠CD,则该四边形 “十字形”.(填“是”或“不是”)
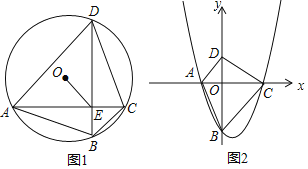
(2)如图1,A,B,C,D是半径为1的⊙O上按逆时针方向排列的四个动点,AC与BD交于点E,∠ADB﹣∠CDB=∠ABD﹣∠CBD,当6≤AC2+BD2≤7时,求OE的取值范围;
(3)如图2,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a,b,c为常数,a>0,c<0)与x轴交于A,C两点(点A在点C的左侧),B是抛物线与y轴的交点,点D的坐标为(0,﹣ac),记“十字形”ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为S1,S2,S3,S4.求同时满足下列三个条件的抛物线的解析式;
①![]() =
=![]()
![]() ;②
;②![]()
![]() =
=![]()
![]() ;③“十字形”ABCD的周长为12
;③“十字形”ABCD的周长为12![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
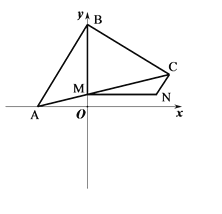
【题目】如图,平面直角坐标系中,A是x轴负半轴上一定点,一动点B从原点出发,沿y轴正半轴运动,以B为直角顶点,作等腰直角三角形△ABC.
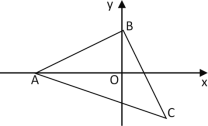
(1) 若B点 运动2秒钟,C点坐标为(2,-2),求A点的坐标;
(2) 如图,B点从(1)中的位置出发保持运动速度不变,再运动2秒钟.E在原B点上,连AE,OD⊥AE,交x轴的平行线DB于D点,求D点坐标
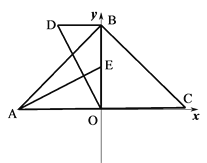
(3) 点B从(2)的位置出发继续运动,如图AC交y轴于M,MN⊥y轴,且BM=MN,连CN,试问:AB和CN是否有某种确定的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AC上取点B,在其同一侧作两个等边三角形△ABD 和△BCE ,连接AE,CD与GF,下列结论正确的有( )

① AE DC;②AHC120;③△AGB≌△DFB;④BH平分AHC;⑤GF∥AC
A.①②④B.①③⑤C.①③④⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简求值:(a-b)(a+b)+a(2b-a),其中a=![]() ,b=-2
,b=-2
(2)已知x2-2x=1,求(x-1)(3x+1)-(x+1)2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com