
【题目】如图,直线AC上取点B,在其同一侧作两个等边三角形△ABD 和△BCE ,连接AE,CD与GF,下列结论正确的有( )

① AE DC;②AHC120;③△AGB≌△DFB;④BH平分AHC;⑤GF∥AC
A.①②④B.①③⑤C.①③④⑤D.①②③④⑤
【答案】D
【解析】
根据等边三角形的性质得到BA=BD,BE=BC,∠ABD=∠CBE=60°,则可根据”SAS“判定△ABE≌△DBC,所以AE=DC,于是可对①进行判断;根据全等三角形的性质得到∠BAE=∠BDC,则可得到∠BAH+∠BCH=60°,从而根据三角形内角和得到∠AHC=120°,则可对②进行判断;利用”ASA”可证明△AGB≌△DFB,从而可对③进行判断;利用△ABE≌△DBC得到AE和DC边上的高相等,则根据角平分线的性质定理逆定理可对④进行判断;证明△BGF为等边三角形得到∠BGF=60°,则∠ABG=∠BGF,所以GF∥AC,从而可对⑤进行判断.
解:∵△ABD和△BCE都是等边三角形,
∴BA=BD,BE=BC,∠ABD=∠CBE=60°,
∵∠DBE=180°60°60°=60°,
∴∠ABE=∠DBC=120°,
∵BA=BD,∠ABD=∠DBC,BE=BC,
∴△ABE≌△DBC(SAS),
∴AE=DC,所以①正确;
∠BAE=∠BDC,
∵∠BDC+∠BCD=∠ABD=60°,
∴∠BAE+∠BCD=60°,
∴∠AHC=180°(∠BAH+∠BCH)=180°60°=120°,所以②正确;
∵∠BAG=∠BDF,BA=BD,∠ABG=∠DBF=60°,
∴△AGB≌△DFB(ASA);所以③正确;
∵△ABE≌△DBC,
∴AE和DC边上的高相等,
即B点到AE和DC的距离相等,
∴BH平分∠AHC,所以④正确;
∵△AGB≌△DFB,
∴BG=BF,
∵∠GBF=60°,
∴△BGF为等边三角形,
∴∠BGF=60°,
∴∠ABG=∠BGF,
∴GF∥AC,所以⑤正确.
故选D.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行调查,已知抽取的样本中,男生和女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 | 身高 |
|
|
|
|
|
|
|
|
|
|
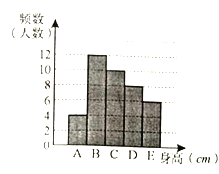
男生身高情况直方图
女生身高情况扇形统计图
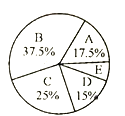
根据图表提供的信息,回答下列问题:
(1)求样本中男生的人数.
(2)求样本中女生身高在E组的人数.
(3)已知该校共有男生380人,女生320人,请估计全校身高在![]() 之间的学生总人数.
之间的学生总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑摩托车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B 村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;
![]()
(2)C村离A村有多远?
(3)若摩托车每100km耗油3升,这趟路共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学在一次实验中统计了某一结果出现的频率,给出的统计图如图所示,则 符合这一结果的实验可能是( )

A. 掷一枚正六面体的骰子,出现6点的概率
B. 掷一枚硬币,出现正面朝上的概率
C. 任意写出一个整数,能被2整除的概率
D. 一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3)

(1)直接写出△ABC的面积为_________
(2)在图形中作出△ABC关于x轴的对称图形△A1B1C1
(3)若△DAB与△CAB全等(D点不与C点重合),则点D的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.

(1)求证:CF=DG;
(2)求出∠FHG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数y=![]() (k>0)图象与AC边交于点E.
(k>0)图象与AC边交于点E.

(1)请用k的表示点E,F的坐标;
(2)若△OEF的面积为9,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,点D的坐标是(0,![]() ),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.
),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A、B两点.
(1)求A、B、C三点的坐标;
(2)求过A、B、C三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过D点,求平移后抛物线的解析式,并指出平移了多少个单位长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com