
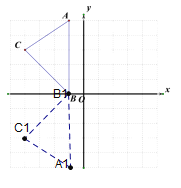
【题目】如图所示,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3)

(1)直接写出△ABC的面积为_________
(2)在图形中作出△ABC关于x轴的对称图形△A1B1C1
(3)若△DAB与△CAB全等(D点不与C点重合),则点D的坐标为__________.
【答案】(1)![]() ;(2)见解析;(3)(-4,2),(2,3),(2,2).
;(2)见解析;(3)(-4,2),(2,3),(2,2).
【解析】
(1)由题得出AB的长及点C到AB的距离,根据三角形面积公式计算即可;
(2)分别作A、B、C三点关于x轴的对称点A1、B1、C1,然后连接A1、B1、C1即可;
(3)由于AB为公共边,再根据全等三角形的性质得出D点位置,写出坐标即可.
(1)由题知AB=5,点C到AB的距离为3,
则S△ABC=5×3×![]() ;
;
(2)分别作A、B、C三点关于x轴的对称点A1、B1、C1,然后连接A1、B1、C1,即为△ABC关于x轴的对称图形△A1B1C1,如图所示:
(3)由于AB为公共边,点C距离AB3个单位长度,![]() ,
,![]() ,
,
当D在AB左侧时,满足条件的为(-4,2),
当D在AB左侧时,满足条件的为(2,3),(2,2),
则△DAB与△CAB全等(D点不与C点重合),则点D的坐标为(-4,2),(2,3),(2,2).


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
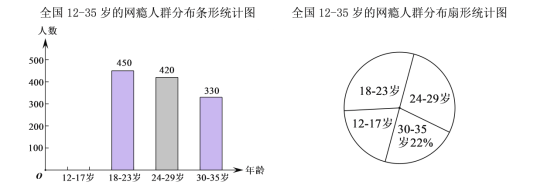
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人,并请补全条形统计图;
(2)扇形统计图中18﹣23岁部分的圆心角的度数是 度;
(3)据报道,目前我国12﹣35岁网瘾人数约为3600万,请估计其中12﹣23岁的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,AB=2,E是DC边上一个动点,F是AB边上一点,∠AEF=30°.设DE=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图所示,则这条线段可能是图中的( ).

A. 线段EC B. 线段AE C. 线段EF D. 线段BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 在数轴上分别表示
在数轴上分别表示![]() .
.
(1)对照数轴填写下表:
| 5 |
|
|
| 3 |
|
| 2 | 0 | 2 |
|
|
|
| 3 | 7 | ________ | 4 | ________ | 0 |
(2)若![]() 两点间的距离记为
两点间的距离记为![]() ,试问
,试问![]() 和
和![]() 有何数量关系?
有何数量关系?
(3)数轴上的整数点为![]() ,它到3和
,它到3和![]() 的距离之和为7,写出这些整数.
的距离之和为7,写出这些整数.
(4)若点![]() 表示的数为
表示的数为![]() ,当点
,当点![]() 在什么位置时,
在什么位置时,![]() 取得的值最小?
取得的值最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AC上取点B,在其同一侧作两个等边三角形△ABD 和△BCE ,连接AE,CD与GF,下列结论正确的有( )

① AE DC;②AHC120;③△AGB≌△DFB;④BH平分AHC;⑤GF∥AC
A.①②④B.①③⑤C.①③④⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为开展“校园读书活动”,雅礼中学读书会计划采购数学文化和文学名著两类书籍共100本. 经了解,购买20 本数学文化和50本文学名著共需1700元, 30本数学文化比30本文学名著贵450 元. (注:所采购的同类书籍价格都一样)
(1)求每本数学文化和文学名著的价格;
(2)若校园读书会要求购买数学文化本数不少于文学名著,且总费用不超过2780元,请求出所有符合条件的购书方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,点E、F分别为射线AC、射线CB上两点,CE=BF,直线EB、AF交于点D.
(1)当E、F在边AC、BC上时如图,求证:△ABF≌△BCE.

(2)当E在AC延长线上时,如图,AC=10,S△ABC=25![]() ,EG⊥BC于G,EH⊥AB于H,HE=8
,EG⊥BC于G,EH⊥AB于H,HE=8![]() ,EG= .
,EG= .

(3)E、F分别在AC、CB延长线上时,如图,BE上有一点P,CP=BD,∠CPB是锐角,求证:BP=AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.

∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2=___(___),
∴AB∥EF(___)
∵∠3=___(___)
又∠B=∠3(已知)
∴∠B=___(等量代换)
∴DE∥BC(___)
∴∠C=∠AED(___).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com