
【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论.

∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2=___(___),
∴AB∥EF(___)
∵∠3=___(___)
又∠B=∠3(已知)
∴∠B=___(等量代换)
∴DE∥BC(___)
∴∠C=∠AED(___).
【答案】∠DFE;同角的补角相等;内错角相等,两直线平行;∠ADE;两直线平行,内错角相等;∠ADE;同位角相等,两直线平行;两直线平行,同位角相等.
【解析】
首先求出∠2=∠DFE,两直线平行可判断出AB∥EF,进而得到∠B=∠ADE,可判断出DE∥BC,由平行线的性质即可得出答案.
∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义),
∴∠2=∠DFE(同角的补角相等),
∴AB∥EF(内错角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
又∠B=∠3(已知),
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠C=∠AED(两直线平行,同位角相等).


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
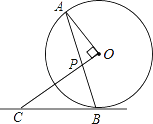
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为![]() ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3)

(1)直接写出△ABC的面积为_________
(2)在图形中作出△ABC关于x轴的对称图形△A1B1C1
(3)若△DAB与△CAB全等(D点不与C点重合),则点D的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
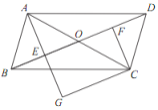
【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数y=![]() (k>0)图象与AC边交于点E.
(k>0)图象与AC边交于点E.

(1)请用k的表示点E,F的坐标;
(2)若△OEF的面积为9,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1.将三角板中30°角的顶点D放在AB边上移动,使这个30°角的两边分别与△ABC的边AC,BC相交于点E,F,且使DE始终与AB垂直.

(1)△BDF是什么三角形?请说明理由;
(2)设AD=x,CF=y,试求y与x之间的函数关系式;(不用写出自变量x的取值范围)
(3)当移动点D使EF∥AB时,求AD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (m为常数,且m≠5).
(m为常数,且m≠5).
(1)若在其图象的每个分支上,y随x的增大而增大,求m的取值范围;
(2)若其图象与一次函数y=-x+1的图象的一个交点的纵坐标是3,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在四边形ABCD中,∠BAD=90°,AD=3cm,AB=4 cm,BC=5 cm, CD=6 cm.
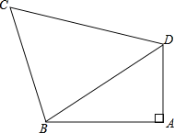
(1)连结BD,判断△CBD的形状;
(2)求四边形ABCD的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元.如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com