
����Ŀ����ͼ,��Rt��ABC��,��ACB=90��,��A=30��,BC=1.�����ǰ���30���ǵĶ���D����AB�����ƶ�,ʹ���30���ǵ����߷ֱ����ABC�ı�AC��BC�ཻ�ڵ�E��F����ʹDEʼ����AB��ֱ.

(1)��BDF��ʲô������?��˵�����ɣ�
(2)��AD=x,CF=y,����y��x֮��ĺ�����ϵʽ;(����д���Ա���x��ȡֵ��Χ)
(3)���ƶ���DʹEF��ABʱ����AD�ij���
���𰸡���1���ȱ������Σ����ɼ���������2��y=x1����3��AD=![]() .
.
��������
��1������֪�ɵá�FDB=60������B=60�����Ӷ��ɵõ���BDF�ǵȱ������Σ�
��2���ɡ�A=30������ACB=90���ɵ�AB=2BC=2���ٽ�CF=y��BF=1-y�����뼴�ɵó�x��y�Ĺ�ϵ��
��3����EF��ABʱ����CEF=30������FED=��EDA=90����CF=![]() EF��EF=
EF��EF=![]() DF��������㼴�����AD�ij���
DF��������㼴�����AD�ij���
(1)��BDF�ǵȱ������Σ�֤�����£�
��ED��AB,��EDF=30��,���FDB=60����
�ߡ�A=30��,��ACB=90��,���B=60����
���DFB=60����
���BDF�ǵȱ������Ρ�
(2)�ߡ�A=30��,��ACB=90����
��AB=2BC=2��
��CF=y��
��BF=1y������BDF�ǵȱ������Σ�
��BD=BF=1y��
��x=2(1y)=1+y��
��y=x1��
(3)��EF��ABʱ,��CEF=30��,��FED=��EDA=90����
��CF=![]() EF,EF=
EF,EF=![]() DF��
DF��
��DF=BF=1y,
��y=![]() (1y),
(1y),
��y=![]() ��
��
��x=y+1=![]() ,��AD=
,��AD=![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���AΪԲ�ģ�AB�ij�Ϊ�뾶��Բǡ����CD�����ڵ�C����AD�ڵ�E���ӳ�BA����A�ཻ�ڵ�F����![]() �ij�Ϊ
�ij�Ϊ![]() ����ͼ����Ӱ���ֵ������
����ͼ����Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��չ��У��������������ѧ�����ƻ��ɹ���ѧ�Ļ�����ѧ���������鼮��100��. ���˽⣬����20 ����ѧ�Ļ���50����ѧ��������1700Ԫ�� 30����ѧ�Ļ���30����ѧ������450 Ԫ. ��ע�����ɹ���ͬ���鼮�۸�һ����
��1����ÿ����ѧ�Ļ�����ѧ�����ļ۸�
��2����У�����Ҫ������ѧ�Ļ�������������ѧ���������ܷ��ò�����2780Ԫ����������з��������Ĺ��鷽����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(12��)ƽ���ı���ABCD��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ������A(��4��0)��B(2��0)��C(3��3)������������y��![]() ��ͼ����C.
��ͼ����C.
(1)��˷����������Ľ���ʽ��
(2)��ƽ���ı���ABCD��x�ᷭ�۵õ�ƽ���ı���ABC��D������˵����D����˫�����ϣ�
(3)����AC��CD��������ACD���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��1+��2=180������3=��B�����жϡ�AED���C�Ĵ�С��ϵ����֤����Ľ���.

��C���AED��ȣ��������£�
�ߡ�1+��2=180��(��֪),��1+��DFE=180��(�ڲ��Ƕ���)
���2=___(___)��
��AB��EF(___)
�ߡ�3=___(___)
�֡�B=��3(��֪)
���B=___(��������)
��DE��BC(___)
���C=��AED(___).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A����4��0����B����3����3����C��0����5��
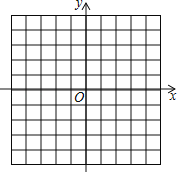
��1��������ABC��
��2����A��B��C������ABC����ƽ�Ƶõ��ģ���ABC������һ��P��x1��y1��ƽ�ƺ�Ķ�Ӧ��ΪP����x1+5��y1+3��������ƽ�ƺ����A��B��C����������A��B��C���������
��3����ֱ��A��C����x�ύ�ڵ�Q����Q���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�У�BC=6![]() ,����AG��BC����E�ӵ�A����������AG��
,����AG��BC����E�ӵ�A����������AG��![]() ���ٶ��˶���ͬʱ��F�ӵ�B����������BC��
���ٶ��˶���ͬʱ��F�ӵ�B����������BC��![]() ���ٶ��˶������˶�ʱ��Ϊ
���ٶ��˶������˶�ʱ��Ϊ![]()

��1������EF����EF����AC�ߵ��е�Dʱ����֤����ADE�ա�CDF
��2����գ�
����![]() Ϊ sʱ���ı���ACFE�����Σ�
Ϊ sʱ���ı���ACFE�����Σ�
����![]() Ϊ sʱ����A��F��C��EΪ������ı�����ֱ�����Σ�
Ϊ sʱ����A��F��C��EΪ������ı�����ֱ�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2+��m+2��x+2m-1=0.
��1����֤��������������ȵ�ʵ����.
��2����mΪ��ֵʱ�����̵�������Ϊ�෴�����������ʱ���̵Ľ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�CD��AB������ΪD��E��AC����һ�㣬EH��AB������ΪH����1����2��
��1����˵��DF��AC��
��2������A��38������BCD��45�������3�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com