
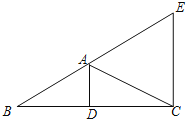
【题目】如图,在△ABC中,AD是边BC上的中线,∠BAD=∠CAD,CE∥AD,CE交BA的延长线于点E,BC=8,AD=3.
(1)求CE的长;
(2)求证:△ABC为等腰三角形.
(3)求△ABC的外接圆圆心P与内切圆圆心Q之间的距离.
【答案】(1)CE=6;(2)证明见解析;(3)△ABC的外接圆圆心P与内切圆圆心Q之间的距离为![]() .
.
【解析】(1)证明AD为△BCE的中位线得到CE=2AD=6;
(2)通过证明△ABD≌△CAD得到AB=AC;
(3)如图,连接BP、BQ、CQ,先利用勾股定理计算出AB=5,设⊙P的半径为R,⊙Q的半径为r,在Rt△PBD中利用勾股定理得到(R-3)2+42=R2,解得R=![]() ,则PD=
,则PD=![]() ,再利用面积法求出r=
,再利用面积法求出r=![]() ,即QD=
,即QD=![]() ,然后计算PD+QD即可.
,然后计算PD+QD即可.
详(1)解:∵AD是边BC上的中线,
∴BD=CD,
∵CE∥AD,
∴AD为△BCE的中位线,
∴CE=2AD=6;
(2)证明:∵BD=CD,∠BAD=∠CAD,AD=AD,
∴△ABD≌△CAD,
∴AB=AC,
∴△ABC为等腰三角形.
(3)如图,连接BP、BQ、CQ,
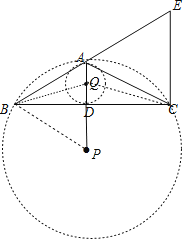
在Rt△ABD中,AB=![]() =5,
=5,
设⊙P的半径为R,⊙Q的半径为r,
在Rt△PBD中,(R-3)2+42=R2,解得R=![]() ,
,
∴PD=PA-AD=![]() -3=
-3=![]() ,
,
∵S△ABQ+S△BCQ+S△ACQ=S△ABC,
∴![]() ×r×5+
×r×5+![]() ×r×8+
×r×8+![]() ×r×5=
×r×5=![]() ×3×8,解得r=
×3×8,解得r=![]() ,
,
即QD=![]() ,
,
∴PQ=PD+QD=![]() +
+![]() =
=![]() .
.
答:△ABC的外接圆圆心P与内切圆圆心Q之间的距离为![]() .
.


科目:初中数学 来源: 题型:
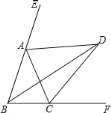
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°∠ABD;④BD平分∠ADC;⑤∠BDC=![]() ∠BAC.其中正确的结论有__________(填序号)
∠BAC.其中正确的结论有__________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在他家里的时钟上安装了一个电脑软件,他设定当钟声在n点钟响起后,下一次则在(3n﹣1)小时后响起,例如钟声第一次在3点钟响起,那么第2次在(3×3﹣1=8)小时后,也就是11点响起,第3次在(3×11﹣1=32)小时后,即7点响起,以此类推…;现在第1次钟声响起时为2点钟,那么第3次响起时为_____点,第2017次响起时为_____点(如图钟表,时间为12小时制).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,点P在边AC上以1cm/s的速度从点A向终点C运动,与此同时点Q在边AB上以同样的速度从点B向终点A运动,各自到达终点后停止运动,设运动时间为t(s),则当△APQ是直角三角形时,t的值为( )
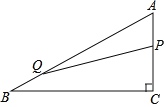
A.2sB.4sC.2s或4sD.2s或4.5s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4cm,动点P从A点出发,在正方形的边上沿A→B→C→D运动,设运动的时间为t(s),△APD的面积为S(cm2),S与t的函数图象如图所示,请回答下列问题:
(1)点P在AB上运动时间为 s,在CD上运动的速度为 cm/s,△APD的面积S的最大值为 cm2;
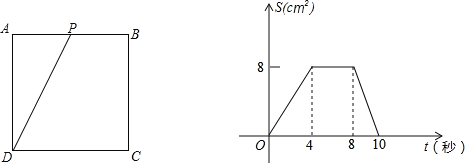
(2)将S与t之间的函数关系式补充完整S=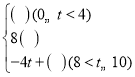 ;
;
(3)请求出运动时间t为几秒时,△APD的面积为6cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AB=CB, BD=BE, ∠ABC=∠DBE=α.



(1)当α=60°, 如图则,∠DPE的度数______________
(2)若△BDE绕点B旋转一定角度,如图所示,求∠DPE(用α表示)
(3)当α=90°,其他条件不变,F为AD的中点,求证 :EC ⊥ BF
查看答案和解析>>
科目:初中数学 来源: 题型:
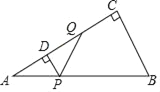
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D(点P不与点A、B重合),作∠DPQ=60°,边PQ交射线DC于点Q.设点P的运动时间为t秒.
(1)用含t的代数式表示线段DC的长;
(2)当点Q与点C重合时,求t的值;
(3)设△PDQ与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式;
(4)当线段PQ的垂直平分线经过△ABC一边中点时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一次函数y=mx+2的图象经过点(﹣2,6).
(1)求m的值;
(2)画出此函数的图象;
(3)平移此函数的图象,使得它与两坐标轴所围成的图形的面积为4,请直接写出此时图象所对应的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com