
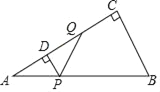
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D(点P不与点A、B重合),作∠DPQ=60°,边PQ交射线DC于点Q.设点P的运动时间为t秒.
(1)用含t的代数式表示线段DC的长;
(2)当点Q与点C重合时,求t的值;
(3)设△PDQ与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式;
(4)当线段PQ的垂直平分线经过△ABC一边中点时,直接写出t的值.
【答案】(1)CD= 2![]() ﹣
﹣![]() t(0<t<2);(2)1;(3)见解析;(4)t的值为
t(0<t<2);(2)1;(3)见解析;(4)t的值为![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)先求出AC,用三角函数求出AD,即可得出结论;
(2)利用AD+DQ=AC,即可得出结论;
(3)分两种情况,利用三角形的面积公式和面积差即可得出结论;
(4)分三种情况,利用锐角三角函数,即可得出结论.
(1)在Rt△ABC中,∠A=30°,AB=4,
∴AC=2![]() ,
,
∵PD⊥AC,
∴∠ADP=∠CDP=90°,
在Rt△ADP中,AP=2t,
∴DP=t,AD=APcosA=2t×![]() =
=![]() t,
t,
∴CD=AC﹣AD=2![]() ﹣
﹣![]() t(0<t<2);
t(0<t<2);
(2)在Rt△PDQ中,∵∠DPC=60°,
∴∠PQD=30°=∠A,
∴PA=PQ,
∵PD⊥AC,
∴AD=DQ,
∵点Q和点C重合,
∴AD+DQ=AC,
∴2×![]() t=2
t=2![]() ,
,
∴t=1;
(3)当0<t≤1时,S=S△PDQ=![]() DQ×DP=
DQ×DP=![]() ×
×![]() t×t=
t×t=![]() t2,
t2,
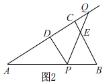
当1<t<2时,如图2,
CQ=AQ﹣AC=2AD﹣AC=2![]() t﹣2
t﹣2![]() =2
=2![]() (t﹣1),
(t﹣1),
在Rt△CEQ中,∠CQE=30°,
∴CE=CQtan∠CQE=2![]() (t﹣1)×
(t﹣1)×![]() =2(t﹣1),
=2(t﹣1),
∴S=S△PDQ﹣S△ECQ=![]() ×
×![]() t×t﹣
t×t﹣![]() ×2
×2![]() (t﹣1)×2(t﹣1)=﹣
(t﹣1)×2(t﹣1)=﹣![]() t2+4
t2+4![]() t﹣2
t﹣2![]() ,
,
∴S=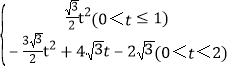 ;
;
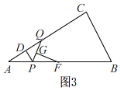
(4)当PQ的垂直平分线过AB的中点F时,如图3,
∴∠PGF=90°,PG=![]() PQ=
PQ=![]() AP=t,AF=
AP=t,AF=![]() AB=2,
AB=2,
∵∠A=∠AQP=30°,
∴∠FPG=60°,
∴∠PFG=30°,
∴PF=2PG=2t,
∴AP+PF=2t+2t=2,
∴t=![]() ;
;
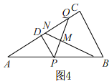
当PQ的垂直平分线过AC的中点M时,如图4,
∴∠QMN=90°,AN=![]() AC=
AC=![]() ,QM=
,QM=![]() PQ=
PQ=![]() AP=t,
AP=t,
在Rt△NMQ中,NQ=![]() ,
,
∵AN+NQ=AQ,
∴![]() +
+![]() =2
=2![]() t,
t,
∴t=![]() ,
,
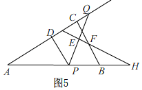
当PQ的垂直平分线过BC的中点时,如图5,
∴BF=![]() BC=1,PE=
BC=1,PE=![]() PQ=t,∠H=30°,
PQ=t,∠H=30°,
∵∠ABC=60°,
∴∠BFH=30°=∠H,
∴BH=BF=1,
在Rt△PEH中,PH=2PE=2t,
∴AH=AP+PH=AB+BH,
∴2t+2t=5,
∴t=![]() ,
,
即:当线段PQ的垂直平分线经过△ABC一边中点时,t的值为![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.


科目:初中数学 来源: 题型:
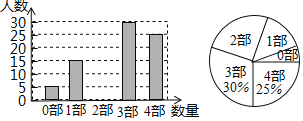
【题目】中华文化源远流长,在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中抽取n名学生进行调查.根据调查结果绘制成如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
(1)求n的值;
(2)请将条形统计图补充完整;
(3)若该校共有2000名学生,请估计该校四大古典名著均已读完的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
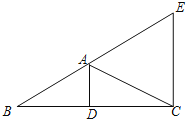
【题目】如图,在△ABC中,AD是边BC上的中线,∠BAD=∠CAD,CE∥AD,CE交BA的延长线于点E,BC=8,AD=3.
(1)求CE的长;
(2)求证:△ABC为等腰三角形.
(3)求△ABC的外接圆圆心P与内切圆圆心Q之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A是x轴负半轴上一定点,一动点B从原点出发,沿y轴正半轴运动,以B为直角顶点,作等腰直角三角形△ABC.
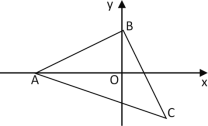
(1) 若B点 运动2秒钟,C点坐标为(2,-2),求A点的坐标;
(2) 如图,B点从(1)中的位置出发保持运动速度不变,再运动2秒钟.E在原B点上,连AE,OD⊥AE,交x轴的平行线DB于D点,求D点坐标
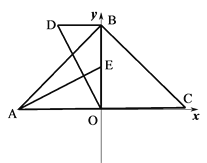
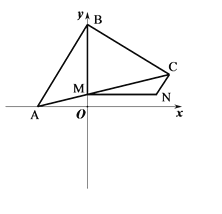
(3) 点B从(2)的位置出发继续运动,如图AC交y轴于M,MN⊥y轴,且BM=MN,连CN,试问:AB和CN是否有某种确定的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AC上取点B,在其同一侧作两个等边三角形△ABD 和△BCE ,连接AE,CD与GF,下列结论正确的有( )

① AE DC;②AHC120;③△AGB≌△DFB;④BH平分AHC;⑤GF∥AC
A.①②④B.①③⑤C.①③④⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠POQ=30°,点A、B在射线OQ上(点A在点O、B之间),半径长为2的⊙A与直线OP相切,半径长为3的⊙B与⊙A相交,那么OB的取值范围是( )
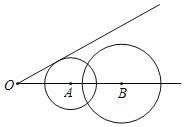
A. 5<OB<9 B. 4<OB<9 C. 3<OB<7 D. 2<OB<7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简求值:(a-b)(a+b)+a(2b-a),其中a=![]() ,b=-2
,b=-2
(2)已知x2-2x=1,求(x-1)(3x+1)-(x+1)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
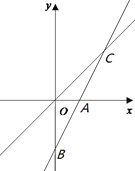
【题目】如图,在平面直角坐标系中,一次函数y=kx+ b的图象分别与x轴和y轴交于点A、B(0,-2),与正比例函数y=x的图象交于点C(m,2).
(1)求m的值和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出使函数y =kx +b的值大于函数y=x的值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
(2)判断△ABC是什么形状?并所明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com