
【题目】如图,在平面直角坐标系中,一次函数y=kx+ b的图象分别与x轴和y轴交于点A、B(0,-2),与正比例函数y=x的图象交于点C(m,2).
(1)求m的值和一次函数的解析式;
(2)求△AOC的面积;
(3)直接写出使函数y =kx +b的值大于函数y=x的值的自变量x的取值范围.
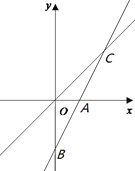
【答案】(1)m=2;y =2x﹣2;(2)S△AOC=1;(3)x>2.
【解析】
(1)把C(m,2)代入y=x得m=2,可得C的坐标,且已知B点的坐标,即可求得一次函数解析式为y = 2x﹣2.
(2) 把y=0代入y=2x﹣2得x=1,则可得A点坐标,即可求得△AOC的面积.
(3) 根据一次函数图形,可知y =kx +b的值大于函数y=x的值,即为自变量x的取值范围是x>2.
解:(1)把C(m,2)代入y=x得m=2,
则点C的坐标为(2,2),
把C(2,2),B(0, -2)代入y = kx + b得![]()
解得![]()
所以一次函数解析式为y = 2x﹣2;
(2)把y=0代入y=2x﹣2得x=1,则A点坐标为(1,0),
所以S△AOC=![]() ×2×1=1;
×2×1=1;
(3)根据一次函数图形,可知y =kx +b的值大于函数y=x的值,即为自变量x的取值范围是x>2.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,点P在边AC上以1cm/s的速度从点A向终点C运动,与此同时点Q在边AB上以同样的速度从点B向终点A运动,各自到达终点后停止运动,设运动时间为t(s),则当△APQ是直角三角形时,t的值为( )
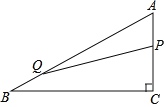
A.2sB.4sC.2s或4sD.2s或4.5s
查看答案和解析>>
科目:初中数学 来源: 题型:
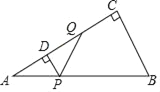
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,动点P从点A出发,沿AB以每秒2个单位长度的速度向终点B运动.过点P作PD⊥AC于点D(点P不与点A、B重合),作∠DPQ=60°,边PQ交射线DC于点Q.设点P的运动时间为t秒.
(1)用含t的代数式表示线段DC的长;
(2)当点Q与点C重合时,求t的值;
(3)设△PDQ与△ABC重叠部分图形的面积为S,求S与t之间的函数关系式;
(4)当线段PQ的垂直平分线经过△ABC一边中点时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,一个点从原点O出发,按向右→向上→向右→向下的顺序依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移到点A1,第二次移到点A2,第三次移到点A3,…,第n次移到点An,则点A2019的坐标是_____________.
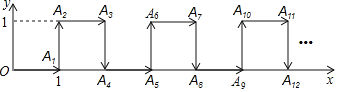
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“一带一路”国际合作高峰论坛在北京举行,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区.已知甲种商品的销售单价为900元,乙种商品的销售单价为600元.
(1)已知乙种商品的销售量不能低于甲种商品销售量的三分之一,则最多能销售甲种商品多少万件?
(2)在(1)的条件下,要使甲、乙两种商品的销售总收入不低于5700万元,请求甲种商品销售量的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一次函数y=mx+2的图象经过点(﹣2,6).
(1)求m的值;
(2)画出此函数的图象;
(3)平移此函数的图象,使得它与两坐标轴所围成的图形的面积为4,请直接写出此时图象所对应的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民李明上星期六买进春兰公司股票1000股,每股27元.下表为本周内每日该股票的涨跌情况(单位:元)(注:本周一股票涨跌是在上周六的基础上,用正数记股价比前一日上升数,用负数记股价比前一日下降数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 | +2 |
(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价每股多少元?
(3)己知李明买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果李明在星期六收盘前将全部股票卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(Ⅰ)求B,C两点间的距离(结果精确到1m);
(Ⅱ)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
参考数据:tan31°≈0.6,tan50°≈1.2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com