练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】（1）化简求值：（a-b）（a+b）+a（2b-a），其中a=，b=-2

    （2）已知x2-2x=1，求（x-1）（3x+1）-（x+1）2的值．

    【答案】（1）-b2+2ab，-10；（2）0

    【解析】

    （1）先按照平方差公式及单项式乘以多项式的运算法则展开化简，再将a=，b=-2代入计算即可．

    （2）先将（x-1）（3x+1）-（x+1）2转化成含有x2-2x的形式，再将x2-2x整体代入求值．

    （1）解：（a+b）（a-b）+a（2b-a）=a2-b2+2ab-a2=-b2+2ab

    当a=，b=-2时；

    原式= -（-2）2+2××（-2）=-4-6=-10

    （2）原式=3x2+x-3x-1-x2-2x-1=2x2-4x-2．
    当x2-2x=1时，
    原式=2（x2-2x）-2=2×1-2=0．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小明在他家里的时钟上安装了一个电脑软件，他设定当钟声在n点钟响起后，下一次则在（3n﹣1）小时后响起，例如钟声第一次在3点钟响起，那么第2次在（3×3﹣1=8）小时后，也就是11点响起，第3次在（3×11﹣1=32）小时后，即7点响起，以此类推…；现在第1次钟声响起时为2点钟，那么第3次响起时为_____点，第2017次响起时为_____点（如图钟表，时间为12小时制）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图, AB=CB, BD=BE, ∠ABC=∠DBE=α.

    (1)当α=60°, 如图则，∠DPE的度数______________

    (2)若△BDE绕点B旋转一定角度，如图所示，求∠DPE（用α表示）

    (3)当α=90°，其他条件不变，F为AD的中点，求证 ：EC ⊥ BF

    查看答案和解析>>

    科目：初中数学 来源： 题型：

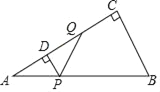
    【题目】如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=4，动点P从点A出发，沿AB以每秒2个单位长度的速度向终点B运动．过点P作PD⊥AC于点D（点P不与点A、B重合），作∠DPQ=60°，边PQ交射线DC于点Q．设点P的运动时间为t秒．

    （1）用含t的代数式表示线段DC的长；

    （2）当点Q与点C重合时，求t的值；

    （3）设△PDQ与△ABC重叠部分图形的面积为S，求S与t之间的函数关系式；

    （4）当线段PQ的垂直平分线经过△ABC一边中点时，直接写出t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，AB∥CD，试解决下列问题：

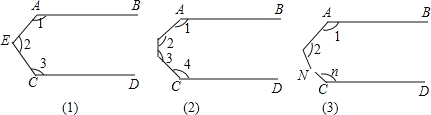
    （1）图（1）中，∠1+∠2+∠3= ；

    （2）图（2）中，∠1+∠2+∠3+∠4= ；

    （3）图（3）中，∠1+∠2+∠3+…+∠n= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，AB=10，点E、F是正方形内两点，AE=FC=6,BE=DF=8,则EF的长为( )

    A. B. C. D. 3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

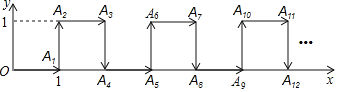
    【题目】如图，平面直角坐标系中，一个点从原点O出发，按向右→向上→向右→向下的顺序依次不断移动，每次移动1个单位，其移动路线如图所示，第1次移到点A1，第二次移到点A2，第三次移到点A3，…，第n次移到点An，则点A2019的坐标是_____________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一次函数y=mx+2的图象经过点（﹣2，6）．

    （1）求m的值；

    （2）画出此函数的图象；

    （3）平移此函数的图象，使得它与两坐标轴所围成的图形的面积为4，请直接写出此时图象所对应的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

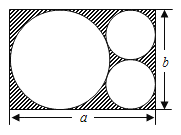
    【题目】如图，在一张长为a、宽为b的长方形纸片上，剪掉一个大圆和两个半径相等的小圆．

    （1）列出剩余纸片（图中阴影部分）面积的代数式；（结果要求化简）

    （2）当a＝6cm，b＝4cm时，求阴影部分的面积，（π取3.14）

    查看答案和解析>>

    同步练习册答案