
【题目】如图1,经过原点O的抛物线y=ax2+bx(a、b为常数,a≠0)与x轴相交于另一点A(3,0).直线l:y=x在第一象限内和此抛物线相交于点B(5,t),与抛物线的对称轴相交于点C.
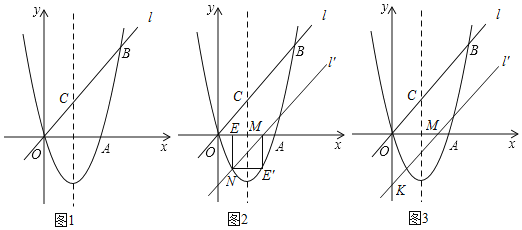
(1)求抛物线的解析式;
(2)在x轴上找一点P,使以点P、O、C为顶点的三角形与以点A、O、B为顶点的三角形相似,求满足条件的点P的坐标;
(3)直线l沿着x轴向右平移得到直线l′,l′与线段OA相交于点M,与x轴下方的抛物线相交于点N,过点N作NE⊥x轴于点E.把△MEN沿直线l′折叠,当点E恰好落在抛物线上时(图2),求直线l′的解析式;
(4)在(3)问的条件下(图3),直线l′与y轴相交于点K,把△MOK绕点O顺时针旋转90°得到△M′OK′,点F为直线l′上的动点.当△M'FK′为等腰三角形时,求满足条件的点F的坐标.
【答案】(1)抛物线的解析式为:y=![]() ;(2)点P坐标为(5,0)或(
;(2)点P坐标为(5,0)或(![]() ,0)(3)y=x﹣2;(4)F坐标为(1,0)或(﹣1,﹣2).
,0)(3)y=x﹣2;(4)F坐标为(1,0)或(﹣1,﹣2).
【解析】(1)应用待定系数法进行求解即可得;
(2)分两种情况△OBA∽△OCP、△OBA∽△OPC分别讨论进行求解即可;
(3)由已知直线l′与x轴所夹锐角为45°,△EMN为等腰直角三角形,当沿直线l′折叠时,四边形ENE′M为正方形,表示点N、E′坐标带入抛物线解析式,可解;
(4)由(3)图形旋转可知,M′K′⊥直线l′,△M'FK′只能为等腰直角三角形,则分类讨论可求解.
(1)由已知点B坐标为(5,5)
把点B(5,5),A(3,0)代入y=ax2+bx,得
![]() ,解得:
,解得: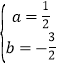 ,
,
∴抛物线的解析式为:y=![]() ;
;
(2)由(1)抛物线对称轴为直线x=![]() ,则点C坐标为(
,则点C坐标为(![]() ,
,![]() ),
),
∴OC=![]() ,OB=5
,OB=5![]() ,
,
当△OBA∽△OCP时,![]() ,∴
,∴![]() ,∴OP=
,∴OP=![]() ,
,
当△OBA∽△OPC时,![]() ,∴
,∴![]() ,∴OP=5,
,∴OP=5,
∴点P坐标为(5,0)或(![]() ,0);
,0);
(3)设点N坐标为(a,b),直线l′解析式为:y=x+c,
∵直线l′y=x+c与x轴夹角为45°,
∴△MEN为等腰直角三角形,
当把△MEN沿直线l′折叠时,四边形ENE′M为正方形,
∴点′E坐标为(a﹣b,b),
∵EE′平行于x轴,
∴E、E′关于抛物线对称轴对称,
∵![]() ,
,
∴b=2a﹣3,
则点N坐标可化为(a,2a﹣3),
把点N坐标代入y=![]() 得:2a﹣3=
得:2a﹣3=![]() ,
,
解得:a1=1,a2=6,
∵a=6时,b=2a﹣3=﹣9<0,
∴a=6舍去,
则点N坐标为(1,﹣1),
把N坐标带入y=x+c,则c=﹣2,
∴直线l′的解析式为:y=x﹣2;
(4)由(3)K点坐标为(0,﹣2),
则△MOK为等腰直角三角形,
∴△M′OK′为等腰直角三角形,M′K′⊥直线l′,
∴当M′K′=M′F时,△M'FK′为等腰直角三角形,
∴F坐标为(1,0)或(﹣1,﹣2).


科目:初中数学 来源: 题型:
【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护环境人人有责,垃圾分类从我做起.某市环保部门为了解垃圾分类的实施情况,抽样调查了部分居民小区一段时间内的生活垃圾分类,对数据进行整理后绘制了如下两幅统计图(其中A表示可回收垃圾,B表示厨余垃圾,C表示有害垃圾,D表示其它垃圾)
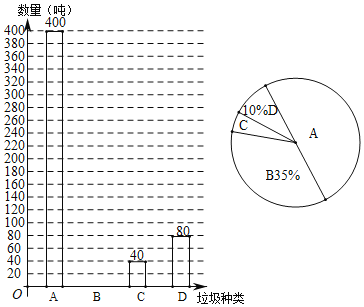
根据图表解答下列问题
(1)这段时间内产生的厨余垃圾有多少吨?
(2)在扇形统计图中,A部分所占的百分比是多少?C部分所对应的圆心角度数是多少?
(3)其它垃圾的数量是有害垃圾数量的多少倍?条形统计图中表现出的直观情况与此相符吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班对道德与法治,历史,地理三门程的选考情况进行调研,数据如下:
科目 | 道德与法治 | 历史 | 地理 |
选考人数(人) | 19 | 13 | 18 |
其中道德与法治,历史两门课程都选了的有3人,历史,地理两门课程都选了的有4人,该班至多有多少学生( )
A.41B.42C.43D.44
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在他家里的时钟上安装了一个电脑软件,他设定当钟声在n点钟响起后,下一次则在(3n﹣1)小时后响起,例如钟声第一次在3点钟响起,那么第2次在(3×3﹣1=8)小时后,也就是11点响起,第3次在(3×11﹣1=32)小时后,即7点响起,以此类推…;现在第1次钟声响起时为2点钟,那么第3次响起时为_____点,第2017次响起时为_____点(如图钟表,时间为12小时制).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班共50名同学,统一参加区教育局举办的防“雾霾”知识检验,成绩分别记作60分、70分、80分、90分、100分,现统计出80分、90分、100分的人数,制成不完整的扇形统计图.
(1)若n=108,则60分的人数为 ;
(2)若从这50份试卷中,随机抽取一份,求抽到试卷的分数低于80分的概率;
(3)若成绩的唯一众数为80分,求这个班平均成绩的最大值.
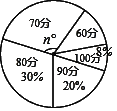
查看答案和解析>>
科目:初中数学 来源: 题型:
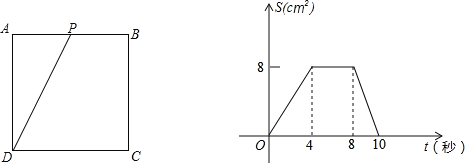
【题目】如图,正方形ABCD的边长为4cm,动点P从A点出发,在正方形的边上沿A→B→C→D运动,设运动的时间为t(s),△APD的面积为S(cm2),S与t的函数图象如图所示,请回答下列问题:
(1)点P在AB上运动时间为 s,在CD上运动的速度为 cm/s,△APD的面积S的最大值为 cm2;
(2)将S与t之间的函数关系式补充完整S=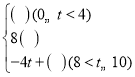 ;
;
(3)请求出运动时间t为几秒时,△APD的面积为6cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,试解决下列问题:
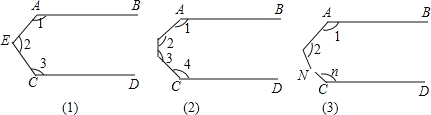
(1)图(1)中,∠1+∠2+∠3= ;
(2)图(2)中,∠1+∠2+∠3+∠4= ;
(3)图(3)中,∠1+∠2+∠3+…+∠n= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com