
【题目】 [问题解决]:如图1,已知AB∥CD,E是直线AB,CD内部一点,连接BE,DE,若∠ABE=40°,∠CDE=60°,求∠BED的度数.
嘉琪想到了如图2所示的方法,但是没有解答完,下面是嘉淇未完成的解答过程:
解:过点E作EF∥AB,
∴∠ABE=∠BEF=40°
∵AB∥CD,
∴EF∥CD,
…
请你补充完成嘉淇的解答过程:
[问题迁移]:请你参考嘉琪的解题思路,完成下面的问题:
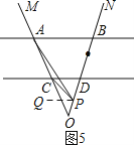
如图3,AB∥CD,射线OM与直线AB,CD分别交于点A,C,射线ON与直线AB,CD分别交于点B,D,点P在射线ON上运动,设∠BAP=α,∠DCP=β.
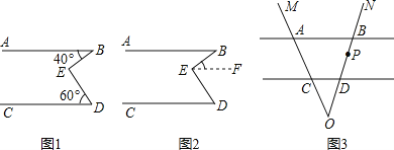
(1)当点P在B,D两点之间运动时(P不与B,D重合),求α,β和∠APC之间满足的数量关系.
(2)当点P在B,D两点外侧运动时(P不与点O重合),直接写出α,β和∠APC之间满足的数量关系.
【答案】[问题解决]见解析;[问题迁移](1) ∠APC=α+β;(2) 当点P在BN上时,∠APC=β-α;当点P在OD上时,∠APC=α-β.
【解析】
问题解决:过点E作EF∥AB,依据平行线的性质,即可得到∠BED的度数;
问题迁移:(1)过P作PQ∥AB,依据平行线的性质,即可得出α,β和∠APC之间满足的数量关系.
(2)分两种情况讨论:过P作PQ∥AB,易得当点P在BN上时,∠APC=β-α;当点P在OD上时,∠APC=α-β.
问题解决:
如图2,过点E作EF∥AB,
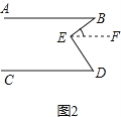
∴∠ABE=∠BEF=40°
∵AB∥CD,
∴EF∥CD,
∴∠B=∠BEF,∠D=∠DEF,
∴∠BED=∠B+∠D=40°+60°=100°;
问题迁移:
(1)如图3,过P作PQ∥AB,
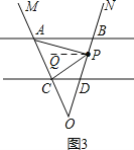
∵AB∥CD,
∴PQ∥CD,
∴∠BAP=∠APQ,∠DCP=∠CPQ,
∴∠APC=∠BAP+∠DCP,即∠APC=α+β;
(2)如图4,当点P在BN上时,∠APC=β-α;
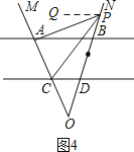
如图5,当点P在OD上时,∠APC=α-β.


科目:初中数学 来源: 题型:
【题目】已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.
(1)如图1,求证:AD=CD;
(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业1~5月份利润的变化情况图所示,以下说法与图中反映的信息相符的是( )
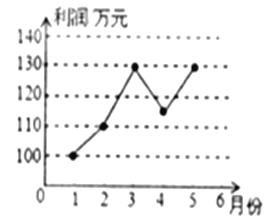
A. 1~3月份利润的平均数是120万元
B. 1~5月份利润的众数是130万元
C. 1~5月份利润的中位数为120万元
D. 1~2月份利润的增长快于2~3月份利润的增长
查看答案和解析>>
科目:初中数学 来源: 题型:
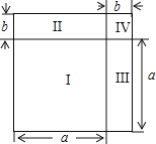
【题目】 在多项式的乘法公式中,完全平方公式是其中重要的一个.
(1)请你补全完全平方公式的推导过程:
(a+b)2=(a+b)(a+b)=a2+______+______+b2=a2+______+b2
(2)如图,将边长为a+b的正方形分割成I,Ⅱ,Ⅲ,Ⅳ四部分,请用不同的方法分别表示出这个正方形的面积,并结合图形给出完全平方公式的几何解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90o,AB=AD,AE=AC, AF⊥CF,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:AC平分∠ECF;
(3)求证:CE=2AF .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门打开的宽度BC为2米,以下哪辆车可以通过?(栏杆宽度,汽车反光镜忽略不计)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)( )
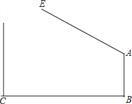
A. 宝马Z4(4200mm×1800mm×1360mm) B. 奔驰smart(4000mm×1600mm×1520mm)
C. 大众朗逸(4600mm×1700mm×1400mm) D. 奥迪A6L(4700mm×1800mm×1400mm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为调动销售人员的积极性,A、B两公司采取如下工资支付方式:A公司每月2000元基本工资,另加销售额的2%作为奖金;B公司每月1600元基本工资,另加销售额的4%作为奖金。已知A、B公司两位销售员小李、小张1~6月份的销售额如下表:
月份 销售额 | 销售额(单位:元) | |||||
1月 | 2月 | 3月 | 4月 | 5月 | 6月 | |
小李(A公司) | 11600 | 12800 | 14000 | 15200 | 16400 | 17600 |
小张(B公司 | 7400 | 9200 | 1100 | 12800 | 14600 | 16400 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有_________(填序号)
①倒数等于它本身的数只有![]() ;
;
②0既不是正数,又不是负数;
③正数和负数统称有理数;
④相反数等于它本身的数是不存在的;
⑤互为相反数的两个数在数轴上对应的两个点到原点的距离相等;
⑥数轴上的点只能表示有理数;
⑦若一个数是有理数,则这个数不是分数就是整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
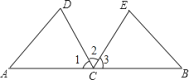
(1)求证:△ACD≌△BCE;
(2)若∠D=75°,求∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com