
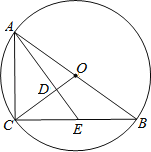
【题目】如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,E为BC上一点,连接AE与OC交于点D,∠CAE=∠CBA.
(1)求证:AE⊥OC;
(2)若⊙O的半径为5,AE的长为6,求AD的长.
【答案】(1)证明见解析;(2)AD=![]() .
.
【解析】
(1)根据直角三角形的性质和垂直的定义即可得到结论;
(2)由△ACE∽△BCA,得到比例式![]() ,设AC=5x,CE=3x,由勾股定理求得AE=
,设AC=5x,CE=3x,由勾股定理求得AE=![]() ,再由三角形相似即可得到结果.
,再由三角形相似即可得到结果.
(1)证明:∵∠ACB=90°,
∴∠CBA+∠CAB=90°,
∵∠CAE=∠CBA,
∴∠CAE+∠CAB=90°,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠CAE+∠ACO=90°,
∴∠ADC=90°,
∴AE⊥OC;
(2)解:∵∠CAE=∠CBA,∠ACB=∠ACE,
∴△ACE∽△BCA,
∴![]() =
=![]() =,
=,
∴设AC=5x,CE=3x,
∴AE=![]() =
=![]() x=6,
x=6,
∴x=![]() ,
,
∴AC=![]() ,
,
∵∠CAE=∠CAD,∠ACE=∠ADC,
∴△ACD∽△AEC,
∴![]() ,
,
∴AD=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
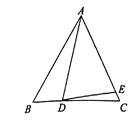
【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE ,设∠BAD=α,∠CDE=β.
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°, 那么α=_______,β=_______.
②求α、β之间的关系式.
(2)是否存在不同于以上②中的α、β之间的关系式?若存在,求出这个关系式,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=3.当四边形BDEF的周长最小时,点E的坐标是( )
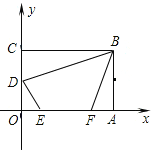
A. (![]() ,0) B. (1,0) C. (
,0) B. (1,0) C. (![]() ,0) D. (2,0)
,0) D. (2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.
(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
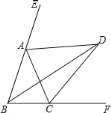
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°∠ABD;④BD平分∠ADC;⑤∠BDC=![]() ∠BAC.其中正确的结论有__________(填序号)
∠BAC.其中正确的结论有__________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护环境人人有责,垃圾分类从我做起.某市环保部门为了解垃圾分类的实施情况,抽样调查了部分居民小区一段时间内的生活垃圾分类,对数据进行整理后绘制了如下两幅统计图(其中A表示可回收垃圾,B表示厨余垃圾,C表示有害垃圾,D表示其它垃圾)
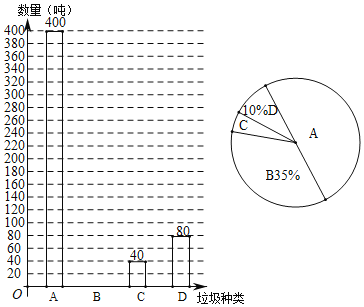
根据图表解答下列问题
(1)这段时间内产生的厨余垃圾有多少吨?
(2)在扇形统计图中,A部分所占的百分比是多少?C部分所对应的圆心角度数是多少?
(3)其它垃圾的数量是有害垃圾数量的多少倍?条形统计图中表现出的直观情况与此相符吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
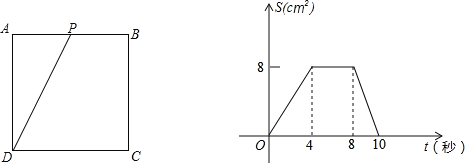
【题目】如图,正方形ABCD的边长为4cm,动点P从A点出发,在正方形的边上沿A→B→C→D运动,设运动的时间为t(s),△APD的面积为S(cm2),S与t的函数图象如图所示,请回答下列问题:
(1)点P在AB上运动时间为 s,在CD上运动的速度为 cm/s,△APD的面积S的最大值为 cm2;
(2)将S与t之间的函数关系式补充完整S=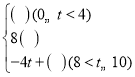 ;
;
(3)请求出运动时间t为几秒时,△APD的面积为6cm2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com