
【题目】△ABC为等边三角形,在平面内找一点P,使△PAB,△PBC,△PAC均为等腰三角形,则这样的点P的个数为_____.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D,E分别在AC,BC上,且CD=CE.
(1)如图1,求证:∠CAE=∠CBD;
(2)如图2,F是BD的中点,求证:AE⊥CF;
(3)如图3,F,G分别是BD,AE的中点,若AC=2![]() ,CE=1,求△CGF的面积.
,CE=1,求△CGF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,直线
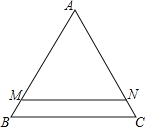
,直线![]() ,且分别交边AB,AC于点M,N,已知直线MN将
,且分别交边AB,AC于点M,N,已知直线MN将![]() 分为
分为![]() 和梯形MBCN面积之比为5:1的两部分,如果将线段AM绕着点A旋转,使点M落在边BC上的点D处,那么
和梯形MBCN面积之比为5:1的两部分,如果将线段AM绕着点A旋转,使点M落在边BC上的点D处,那么![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,b)、点B(a,0)、点D(d,0)且a、b、c满足![]() .DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
.DE⊥x轴且∠BED=∠ABD,BE交y轴于点C,AE交x轴于点F.
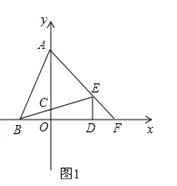
(1)求点A、B、D的坐标;
(2)求点C、E、F的坐标;
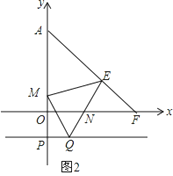
(3)如图,过P(0,-1)作x轴的平行线,在该平行线上有一点Q(点Q在P的右侧)使∠QEM=45°,QE交x轴于N,ME交y轴正半轴于M,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
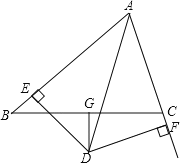
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)判断BE与CF的数量关系,并说明理由;
(2)如果AB=8,AC=6,求AE、BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
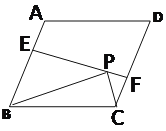
【题目】如图,在菱形ABCD中,sinD=![]() ,E、F分别是AB,CD上的点,BC=5,AE=CF=2,点P是线段EF上一点,则当△BPC时直角三角形时,CP的长为____________
,E、F分别是AB,CD上的点,BC=5,AE=CF=2,点P是线段EF上一点,则当△BPC时直角三角形时,CP的长为____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备到服装超市购一批演出服装(男,女服装价格相同)以供文艺汇演使用,一套服装定价![]() 元,领结(花)每条定价
元,领结(花)每条定价![]() 元,适逢新中国成立
元,适逢新中国成立![]() 周年,服装超市开展促销活动,向客户提供两种优惠方案:
周年,服装超市开展促销活动,向客户提供两种优惠方案:
①买一套服装送一条领结(花);
②服装和领结(花)都按定价的![]() 销售.
销售.
现该校要到该服装超市购买服装![]() 套,领结(花)
套,领结(花)![]() 条
条![]()
![]() .
.
(1)若该校按方案①购买.需付款_______ 元(用含![]() 的式子表示);若该校按方案②购买.需付款 元(用含
的式子表示);若该校按方案②购买.需付款 元(用含![]() 的式子表示);
的式子表示);
(2)若![]() ,通过计算说明此时按哪种方案付款比较合算;
,通过计算说明此时按哪种方案付款比较合算;
(3)当![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并计算出需付款多少元.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并计算出需付款多少元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com