
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,直线
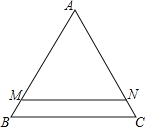
,直线![]() ,且分别交边AB,AC于点M,N,已知直线MN将
,且分别交边AB,AC于点M,N,已知直线MN将![]() 分为
分为![]() 和梯形MBCN面积之比为5:1的两部分,如果将线段AM绕着点A旋转,使点M落在边BC上的点D处,那么
和梯形MBCN面积之比为5:1的两部分,如果将线段AM绕着点A旋转,使点M落在边BC上的点D处,那么![]() ______.
______.
【答案】![]()
【解析】过点A作AE⊥BC于点E,由AB=AC、∠A=60°,可得出△ABC为等边三角形,进而可得出BE、AE的长度,由MN∥BC可得出△AMN∽△ABC,根据相似三角形的性质结合直线MN将△ABC分为△AMN和梯形MBCN面积之比为5:1的两部分,可求出AM的长度,由旋转的性质可得出AD的长度,在Rt△ADE中,利用勾股定理可求出DE的长度,再根据BD=BE±DE,即可求出BD的长度.
过点A作AE⊥BC于点E,如图所示.
∵AB=AC,∠A=60,
∴△ABC为等边三角形,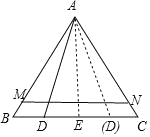
∴BE=CE=![]() BC=3,AE=
BC=3,AE=![]() BC=3
BC=3![]() .
.
∵MN∥BC,
∴△AMN∽△ABC,
∴![]() ,
,
∵直线MN将△ABC分为△AMN和梯形MBCN面积之比为5:1的两部分,
∴![]() =
=![]() ,即
,即![]() ,
,
解得:AM=![]() ,
,
∴AD=AM=![]()
在Rt△ADE中,∠AED=90,AD=![]() ,AE=3
,AE=3![]() .
.
∴DE=3![]() ,
,
∴BD=BE±DE=3±3![]()
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:5:6,③∠A=90°﹣∠B,④∠A=∠B=![]() ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E.将△BDE沿直线DE折叠,得到△B′DE,若B′D,B′E分别交AC于点F,G,连接OF,OG,则下列判断错误的是( )
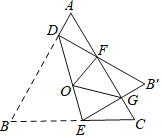
A. △ADF≌△CGE
B. △B′FG的周长是一个定值
C. 四边形FOEC的面积是一个定值
D. 四边形OGB'F的面积是一个定值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=30°,∠AOE=130°,OB平分∠AOC, OD平分∠AOE.
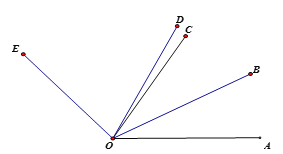
(1)求∠COD的度数;
(2)若以O为观测中心,OA为正东方向,则射线OD的方位角是 ;
(3)若∠AOC、射线OE分别以每秒5°、每秒3°的速度同时绕点O逆时针方向旋转,其他条件不变,当OA回到原处时,全部停止运动,则经过多长时间,∠BOE=28°?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:⊙O是正方形ABCD的外接圆,点E在![]() 上,连接BE、DE,点F在
上,连接BE、DE,点F在![]() 上连接BF、DF,BF与DE、DA分别交于点G、点H,且DA平分∠EDF.
上连接BF、DF,BF与DE、DA分别交于点G、点H,且DA平分∠EDF.
(1)如图1,求证:∠CBE=∠DHG;
(2)如图2,在线段AH上取一点N(点N不与点A、点H重合),连接BN交DE于点L,过点H作HK∥BN交DE于点K,过点E作EP⊥BN,垂足为点P,当BP=HF时,求证:BE=HK;
(3)如图3,在(2)的条件下,当3HF=2DF时,延长EP交⊙O于点R,连接BR,若△BER的面积与△DHK的面积的差为![]() ,求线段BR的长.
,求线段BR的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形ABCD中,∠A=∠C=90°.

(1)如图1,若BE平分∠ABC,DF平分∠ADC的邻补角,请写出BE与DF的位置关系,并证明.
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
(3)如图3,若BE、DE分别六等分∠ABC、∠ADC的邻补角(即∠CBE=![]() ∠CBM,∠CDE=
∠CBM,∠CDE=![]() ∠CDN),则∠E= .
∠CDN),则∠E= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(列方程(组)及不等式解应用题)
水是人类生命之源.为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策.若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,每立方米污水处理费不变.甲用户4月份用水8立方米,缴水费27.6元;乙用户4月份用水12立方米,缴水费46.3元.(注:污水处理的立方数=实际生活用水的立方数)
(1)求每立方米的基本水价和每立方米的污水处理费各是多少元?
(2)如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】概念学习:规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如![]() ,
,![]() 等,类比有理数的乘方,我们把
等,类比有理数的乘方,我们把![]() 记作
记作![]() ,读作“2的圈3次方”,
,读作“2的圈3次方”,![]() 记作
记作![]() ,读作“-3的圈4次方”,一般地,把
,读作“-3的圈4次方”,一般地,把![]() 个
个![]()
![]()
![]() ,记作,读作“
,记作,读作“![]() 的圈
的圈![]() 次方”
次方”
初步探究:直接写出计算结果:![]() ,
,![]() ;
;
深入思考:我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
(1)试一试:仿照下面的算式,将下列运算结果直接写成幂的形式.
例如![]()
![]()
![]()
![]() ;
; ![]() = ;
= ;
(2)想一想:将一个非零有理数![]() 的圈
的圈![]() 次方写成幂的形式等于 ;
次方写成幂的形式等于 ;
(3)算一算:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com