
ЁОЬтФПЁПИХФюбЇЯАЃКЙцЖЈЃКЧѓШєИЩИіЯрЭЌЕФгаРэЪ§ЃЈОљВЛЕШгк0ЃЉЕФГ§ЗЈдЫЫуНазіГ§ЗНЃЌШч![]() ЃЌ
ЃЌ![]() ЕШЃЌРрБШгаРэЪ§ЕФГЫЗНЃЌЮвУЧАб
ЕШЃЌРрБШгаРэЪ§ЕФГЫЗНЃЌЮвУЧАб![]() МЧзї
МЧзї![]() ЃЌЖСзїЁА2ЕФШІ3ДЮЗНЁБЃЌ
ЃЌЖСзїЁА2ЕФШІ3ДЮЗНЁБЃЌ![]() МЧзї
МЧзї![]() ЃЌЖСзїЁА-3ЕФШІ4ДЮЗНЁБЃЌвЛАуЕиЃЌАб
ЃЌЖСзїЁА-3ЕФШІ4ДЮЗНЁБЃЌвЛАуЕиЃЌАб![]() Иі
Иі![]()
![]()
![]() ЃЌМЧзїЃЌЖСзїЁА
ЃЌМЧзїЃЌЖСзїЁА![]() ЕФШІ
ЕФШІ![]() ДЮЗНЁБ
ДЮЗНЁБ
ГѕВНЬНОПЃКжБНгаДГіМЦЫуНсЙћЃК![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЩюШыЫМПМЃКЮвУЧжЊЕРЃЌгаРэЪ§ЕФМѕЗЈдЫЫуПЩвдзЊЛЏЮЊМгЗЈдЫЫуЃЌГ§ЗЈдЫЫуПЩвдзЊЛЏЮЊГЫЗЈдЫЫуЃЌгаРэЪ§ЕФГ§ЗНдЫЫуШчКЮзЊЛЏЮЊГЫЗНдЫЫуФиЃП
ЃЈ1ЃЉЪдвЛЪдЃКЗТееЯТУцЕФЫуЪНЃЌНЋЯТСадЫЫуНсЙћжБНгаДГЩУнЕФаЮЪНЃЎ
Р§Шч![]()
![]()
![]()
![]() ЃЛ
ЃЛ ![]() = ЃЛ
= ЃЛ
ЃЈ2ЃЉЯывЛЯыЃКНЋвЛИіЗЧСугаРэЪ§![]() ЕФШІ
ЕФШІ![]() ДЮЗНаДГЩУнЕФаЮЪНЕШгк ЃЛ
ДЮЗНаДГЩУнЕФаЮЪНЕШгк ЃЛ
ЃЈ3ЃЉЫувЛЫуЃК![]()
ЁОД№АИЁПГѕВНЬНОПЃК![]() ЃЌ-2ЃЛЩюШыЫМПМЃКЃЈ1ЃЉ
ЃЌ-2ЃЛЩюШыЫМПМЃКЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ГѕВНЬНОПЃКжБНгИљОнЖЈвхМДПЩМЦЫуЃЛ
ЩюШыЫМПМЃКЃЈ1ЃЉЗТееР§ЬтМДПЩНтД№ЃЛ
ЃЈ2ЃЉИљОнЃЈ1ЃЉЕФМЦЫуЃЌПЩжБНгВТЯыЕУГіЃЛ
ЃЈ3ЃЉРћгУЃЈ2ЃЉЕФЙЋЪНМАгаРэЪ§ЕФдЫЫуЗЈдђМЦЫуМДПЩЃЎ
НтЃКГѕВНЬНОПЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК![]() ЃЌ-2ЃЛ
ЃЌ-2ЃЛ
ЩюШыЫМПМЃКЃЈ1ЃЉ![]()
![]()
![]()
![]()
=![]()
ЙЪД№АИЮЊЃК![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉЕФМЦЫуПЩЕУЃК![]()
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉ![]()
=![]()
=![]()
=![]()
=![]()


 аТЛюСІзмЖЏдБЪюЯЕСаД№АИ
аТЛюСІзмЖЏдБЪюЯЕСаД№АИ СњШЫЭМЪщПьРжМйЦкЪюМйзївЕжЃжнДѓбЇГіАцЩчЯЕСаД№АИ
СњШЫЭМЪщПьРжМйЦкЪюМйзївЕжЃжнДѓбЇГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌжБЯп
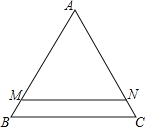
ЃЌжБЯп![]() ЃЌЧвЗжБ№НЛБпABЃЌACгкЕуMЃЌNЃЌвбжЊжБЯпMNНЋ
ЃЌЧвЗжБ№НЛБпABЃЌACгкЕуMЃЌNЃЌвбжЊжБЯпMNНЋ![]() ЗжЮЊ
ЗжЮЊ![]() КЭЬнаЮMBCNУцЛ§жЎБШЮЊ5ЃК1ЕФСНВПЗжЃЌШчЙћНЋЯпЖЮAMШЦзХЕуAа§зЊЃЌЪЙЕуMТфдкБпBCЩЯЕФЕуDДІЃЌФЧУД
КЭЬнаЮMBCNУцЛ§жЎБШЮЊ5ЃК1ЕФСНВПЗжЃЌШчЙћНЋЯпЖЮAMШЦзХЕуAа§зЊЃЌЪЙЕуMТфдкБпBCЩЯЕФЕуDДІЃЌФЧУД![]() ______ЃЎ
______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
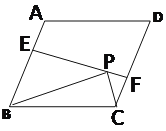
ЁОЬтФПЁПШчЭМ,дкСтаЮABCDжаЃЌsinD=![]() ,EЁЂFЗжБ№ЪЧAB,CDЩЯЕФЕуЃЌBC=5ЃЌAE=CF=2ЃЌЕуPЪЧЯпЖЮEFЩЯвЛЕуЃЌдђЕБЁїBPCЪБжБНЧШ§НЧаЮЪБЃЌCPЕФГЄЮЊ____________
,EЁЂFЗжБ№ЪЧAB,CDЩЯЕФЕуЃЌBC=5ЃЌAE=CF=2ЃЌЕуPЪЧЯпЖЮEFЩЯвЛЕуЃЌдђЕБЁїBPCЪБжБНЧШ§НЧаЮЪБЃЌCPЕФГЄЮЊ____________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬсГіЮЪЬтЃКШчЭМЃЌгавЛПщЗжВМОљдШЕФЕШбќШ§НЧаЮЕАИтЃЈAB=BCЃЌЧвBCЁйACЃЉЃЌдкЕАИтЕФБпдЕОљдШЗжВМзХЧЩПЫСІЃЌаЁУїКЭаЁЛЊОіЖЈжЛЧавЛЕЖНЋетПщЕАИтЦНЗжЃЈвЊЧѓЗжЕУЕФЕАИтКЭЧЩПЫСІжЪСПЖМвЛбљЃЉЃЎ
БГОАНщЩмЃКетЬѕЗжИюжБЯпМДЦНЗжСЫШ§НЧаЮЕФУцЛ§ЃЌгжЦНЗжСЫШ§НЧаЮЕФжмГЄЃЌЮвУЧГЦетЬѕЯпЮЊШ§НЧаЮЕФЁАЕШЗжЛ§жмЯпЁБЃЎГЂЪдНтОіЃК
ЃЈ1ЃЉаЁУїКмПьОЭЯыЕНСЫвЛЬѕЗжИюжБЯпЃЌЖјЧвгУГпЙцзїЭМзїГіЃЎЧыФуАяаЁУїдкЭМ1жаЛГіетЬѕЁАЕШЗжЛ§жмЯпЁБЃЌДгЖјЦНЗжЕАИтЃЎ
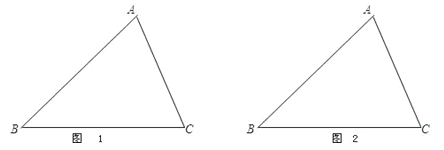
ЃЈ2ЃЉаЁЛЊОѕЕУаЁУїЕФЗНЗЈКмКУЃЌЫљвдздМКФЃЗТзХдкЭМ1жаЙ§ЕуCЛСЫвЛЬѕжБЯпCDНЛABгкЕуDЃЎФуОѕЕУаЁЛЊЛсГЩЙІТ№ШчФмГЩЙІЃЌЫЕГіШЗЖЈЕФЗНЗЈЃЛШчВЛФмГЩЙІЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉЭЈЙ§ЩЯУцЕФЪЕМљЃЌФувЛЖЈгаСЫИќЩюПЬЕФШЯЪЖЃЎЧыФуНтОіЯТУцЕФЮЪЬтЃКШєAB=BC=5cmЃЌAC=6cmЃЌЧыФуевГіЁїABCЕФЫљгаЁАЕШЗжЛ§жмЯпЁБЃЌВЂМђвЊЕФЫЕУїШЗЖЈЕФЗНЗЈЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗжНтвђЪНЃК
(1)Љ3x2y+6xy2Љ12xy
(2)81Љm4
(3)2x2Љ4xy+2y2
(4)(x+2)(xЉ2)Љ5.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГИпаЃбЇЩњЛсЗЂЯжЭЌбЇУЧОЭВЭЪБЪЃгрЗЙВЫНЯЖрЃЌРЫЗббЯжиЃЌгкЪЧзМБИдкаЃФкГЋЕМЁАЙтХЬааЖЏЁБЃЌШУЭЌбЇУЧефЯЇСИЪГЃЌЮЊСЫШУЭЌбЇУЧРэНтетДЮЛюЖЏЕФживЊадЃЌаЃбЇЩњЛсдкФГЬьЮчВЭКѓЃЌЫцЛњЕїВщСЫВПЗжЭЌбЇетВЭЗЙВЫЕФЪЃгрЧщПіЃЌВЂНЋНсЙћЭГМЦКѓЛцжЦГЩСЫШчЭМЫљЪОЕФВЛЭъећЕФЭГМЦЭМЁЃ

(1)етДЮБЛЕїВщЕФЭЌбЇЙВга УћЃЛ
(2)АбЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
(3)аЃбЇЩњЛсЭЈЙ§Ъ§ОнЗжЮіЃЌЙРМЦетДЮБЛЕїВщЕФЫљгабЇЩњвЛВЭРЫЗбЕФЪГЮяПЩвдЙЉ200ШЫгУвЛВЭЁЃОнДЫЙРЫуЃЌИУаЃ18000УћбЇЩњвЛВЭРЫЗбЕФЪГЮяПЩЙЉЖрЩйШЫЪГгУвЛВЭЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃзМБИЕНЗўзАГЌЪаЙКвЛХњбнГіЗўзА(ФаЃЌХЎЗўзАМлИёЯрЭЌ)вдЙЉЮФвеЛубнЪЙгУЃЌвЛЬзЗўзАЖЈМл![]() дЊЃЌСьНс(ЛЈ)УПЬѕЖЈМл
дЊЃЌСьНс(ЛЈ)УПЬѕЖЈМл![]() дЊЃЌЪЪЗъаТжаЙњГЩСЂ
дЊЃЌЪЪЗъаТжаЙњГЩСЂ![]() жмФъЃЌЗўзАГЌЪаПЊеЙДйЯњЛюЖЏЃЌЯђПЭЛЇЬсЙЉСНжжгХЛнЗНАИЃК
жмФъЃЌЗўзАГЌЪаПЊеЙДйЯњЛюЖЏЃЌЯђПЭЛЇЬсЙЉСНжжгХЛнЗНАИЃК
ЂйТђвЛЬзЗўзАЫЭвЛЬѕСьНс(ЛЈ)ЃЛ
ЂкЗўзАКЭСьНс(ЛЈ)ЖМАДЖЈМлЕФ![]() ЯњЪлЃЎ
ЯњЪлЃЎ
ЯжИУаЃвЊЕНИУЗўзАГЌЪаЙКТђЗўзА![]() ЬзЃЌСьНс(ЛЈ)
ЬзЃЌСьНс(ЛЈ)![]() Ьѕ
Ьѕ![]()
![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШєИУаЃАДЗНАИЂйЙКТђЃЎашИЖПю_______ дЊ(гУКЌ![]() ЕФЪНзгБэЪО)ЃЛШєИУаЃАДЗНАИЂкЙКТђЃЎашИЖПю дЊ(гУКЌ
ЕФЪНзгБэЪО)ЃЛШєИУаЃАДЗНАИЂкЙКТђЃЎашИЖПю дЊ(гУКЌ![]() ЕФЪНзгБэЪО)ЃЛ
ЕФЪНзгБэЪО)ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЭЈЙ§МЦЫуЫЕУїДЫЪБАДФФжжЗНАИИЖПюБШНЯКЯЫуЃЛ
ЃЌЭЈЙ§МЦЫуЫЕУїДЫЪБАДФФжжЗНАИИЖПюБШНЯКЯЫуЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌФуФмИјГівЛжжИќЮЊЪЁЧЎЕФЙКТђЗНАИТ№?ЪдаДГіФуЕФЙКТђЗНАИЃЌВЂМЦЫуГіашИЖПюЖрЩйдЊЃЎ
ЪБЃЌФуФмИјГівЛжжИќЮЊЪЁЧЎЕФЙКТђЗНАИТ№?ЪдаДГіФуЕФЙКТђЗНАИЃЌВЂМЦЫуГіашИЖПюЖрЩйдЊЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭтЙњгяжабЇЬхг§зщзМБИдкЭјЩЯЮЊбЇаЃЖЉЙКвЛХњФГЦЗХЦзуЧђКЭЬјЩўЃЌдкВщдФЬьУЈЭјЕъКѓЗЂЯжзуЧђУПСЃЖЈМл![]() дЊЃЌЬјЩўУПИіЖЈМл
дЊЃЌЬјЩўУПИіЖЈМл![]() дЊЃЎЁАЫЋЪЎвЛЁБЦкМф
дЊЃЎЁАЫЋЪЎвЛЁБЦкМф![]() СНМвЭјЕъОљЬсЙЉАќгЪЗўЮёЃЌВЂЬсГіСЫИїздЕФгХЛнЗНАИЃЎ
СНМвЭјЕъОљЬсЙЉАќгЪЗўЮёЃЌВЂЬсГіСЫИїздЕФгХЛнЗНАИЃЎ
![]() ЭјЕуЃКТђвЛСЃзуЧђбЁвЛИіЬјЩўЃЛ
ЭјЕуЃКТђвЛСЃзуЧђбЁвЛИіЬјЩўЃЛ
![]() ЭјЕуЃКзуЧђКЭЬјЩўЖМАДЖЈМлЕФ
ЭјЕуЃКзуЧђКЭЬјЩўЖМАДЖЈМлЕФ![]() ИЖПю
ИЖПю
вбжЊвЊЙКТђзуЧђ![]() СЃЃЌЬјЩў
СЃЃЌЬјЩў![]() Иі(
Иі(![]() )
)
ЃЈ1ЃЉШєдк![]() ЭјЕъЙКТђЃЌашИЖПю дЊЃЎ (гУКЌ
ЭјЕъЙКТђЃЌашИЖПю дЊЃЎ (гУКЌ![]() ЕФДњЪ§ЪНБэЪО)Шєдк
ЕФДњЪ§ЪНБэЪО)Шєдк![]() ЭјЕъЙКТђЃЌашИЖПю дЊЃЎ(гУКЌ
ЭјЕъЙКТђЃЌашИЖПю дЊЃЎ(гУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЎ
ЕФДњЪ§ЪНБэЪО)ЃЎ
ЃЈ2ЃЉШє![]() ЪБЃЌЭЈЙ§МЦЫуЫЕУїДЫЪБдкФФМвЭјЕъЙКТђНЯЮЊКЯЫуЃП
ЪБЃЌЭЈЙ§МЦЫуЫЕУїДЫЪБдкФФМвЭјЕъЙКТђНЯЮЊКЯЫуЃП
ЃЈ3ЃЉЕБ![]() ЪБЃЌФуФмИјГівЛжжИќЮЊЪЁЧЎЕФЙКТђЗНАИТ№ЃПЪдаДГіФуЕФЙКТђЗНЗЈЃЌВЂМЦЫуашИЖПюЖрЩйдЊЃП
ЪБЃЌФуФмИјГівЛжжИќЮЊЪЁЧЎЕФЙКТђЗНАИТ№ЃПЪдаДГіФуЕФЙКТђЗНЗЈЃЌВЂМЦЫуашИЖПюЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌPЮЊЁбOЭтвЛЕуЃЌPAЁЂPBЗжБ№ЧаЁбOгкAЁЂBСНЕуЃЌOPНЛЁбOгкЕуCЃЌСЌНгBOВЂбгГЄНЛЁбOгкЕуDЃЌНЛPAЕФбгГЄЯпгкЕуEЃЌСЌНгADЁЂBCЃЎЯТСаНсТлЃКЂйADЁЮPOЃЛЂкЁїADEЁзЁїPCBЃЛЂлtanЁЯEAD=![]() ЃЛЂмBD2=2ADOPЃЎЦфжавЛЖЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЃЛЂмBD2=2ADOPЃЎЦфжавЛЖЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ

A. ЂйЂлЂм B. ЂкЂм C. ЂйЂкЂл D. ЂйЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com