
【题目】如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,OP交⊙O于点C,连接BO并延长交⊙O于点D,交PA的延长线于点E,连接AD、BC.下列结论:①AD∥PO;②△ADE∽△PCB;③tan∠EAD=![]() ;④BD2=2ADOP.其中一定正确的是( )
;④BD2=2ADOP.其中一定正确的是( )

A. ①③④ B. ②④ C. ①②③ D. ①②③④
【答案】A
【解析】连接OA,如图,
∵PA、PB分别是O的切线,
∴∠APO=∠BPO,OA⊥PA,OB⊥PB;
∴∠2=∠4,
∵OB=OC,
∴∠1=∠3,
∵∠2++∠4=∠1+∠3,
∴∠3=∠4,
∴OP∥AD,所以①正确;
∵OP∥AD,
∴∠ADE=∠POE,
∵∠POE+∠COB=180°,∠PCB+∠OCB=180°,
而∠COB≠∠OCB,
∴∠PCB≠∠POE,
∴∠PCB≠∠ADE,
∴不能判断△ADE∽△PCB,所以②错误;
∵OP∥AD,
∴∠EAD=∠EPO,![]() ,
,
∴![]() ,
,
在Rt△AOP中,∵tan∠APO=![]() ,
,
而OA=OD,
∴tan∠APO=![]() =
=![]() P,
P,
∴tan∠EAD=![]() ,所以③正确;
,所以③正确;
连结AB,如图,∵BD为直径,
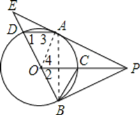
∴∠BAD=90°,
∵OP∥AD,
∴∠ADB=∠POB,
∴Rt△ABD∽△BPO,
∴![]() ,
,
∴![]() BDBD=ADOP,
BDBD=ADOP,
∴BD2=2ADOP,所以④正确。
故选A.


科目:初中数学 来源: 题型:
【题目】概念学习:规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如![]() ,
,![]() 等,类比有理数的乘方,我们把
等,类比有理数的乘方,我们把![]() 记作
记作![]() ,读作“2的圈3次方”,
,读作“2的圈3次方”,![]() 记作
记作![]() ,读作“-3的圈4次方”,一般地,把
,读作“-3的圈4次方”,一般地,把![]() 个
个![]()
![]()
![]() ,记作,读作“
,记作,读作“![]() 的圈
的圈![]() 次方”
次方”
初步探究:直接写出计算结果:![]() ,
,![]() ;
;
深入思考:我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
(1)试一试:仿照下面的算式,将下列运算结果直接写成幂的形式.
例如![]()
![]()
![]()
![]() ;
; ![]() = ;
= ;
(2)想一想:将一个非零有理数![]() 的圈
的圈![]() 次方写成幂的形式等于 ;
次方写成幂的形式等于 ;
(3)算一算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
“十一”黄金周期间,齐齐哈尔市动物园在7天假期中每天接待的人数变化如下表(正数表小比前一天多的人数,负数表示比前一天少的人数):
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化(万人) | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若9月份的最后一天9月30日的游客人数记为![]() 万人,请用含
万人,请用含![]() 的代数式表示10月2日的游客人数;
的代数式表示10月2日的游客人数;
(2)在(1)条件下,请直接写出七天内游客人数最多的是哪天,有多少万人?
(3)若9月30日的游客人数为2万人,门票每人100元,则黄金周期间齐齐哈尔市动物园票收入是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
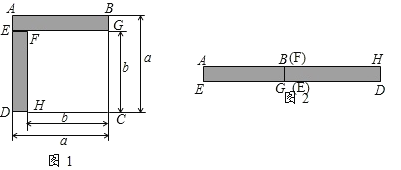
【题目】解决问题:
(1)如图1,已知正方形![]() 的边长为
的边长为![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,长方形
,长方形![]() 和
和![]() 为阴影部分,则阴影部分的面积是____.(写成平方差的形式)
为阴影部分,则阴影部分的面积是____.(写成平方差的形式)
(2)将图1中的长方形![]() 和
和![]() 剪下来,拼成图2所示的长方形,则长方形
剪下来,拼成图2所示的长方形,则长方形![]() 的面积是____.(写成多项式相乘的形式)
的面积是____.(写成多项式相乘的形式)
(3)比较图1与图2的阴影部分的面积,可得乘法公式____.
(4)利用所得公式计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从白塔山山顶A外测得正前方的长江两岸B、C的俯角分别为30°,75°,白塔山的高度AD是600m,则长江的宽度BC等于( )
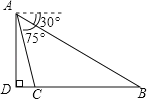
A. 300(![]() +1)m B. 1200(
+1)m B. 1200(![]() ﹣1)m C. 1800(
﹣1)m C. 1800(![]() ﹣1)m D. 2400(
﹣1)m D. 2400(![]() ﹣1)m
﹣1)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,C点在y轴上,B点在x轴上,A点从C点出发沿正西运动,B点在x轴上运动.

(1)如图1当∠ABC=∠ABD,作∠CBO的平分线交AC的延长线于E,作CF⊥EB于F.求证:∠ABD=∠ECF;
(2)如图2,在(1)的条件下,延长AB与∠BCO的平分线交于M点,下列结论:
①∠M的度数不变;
②∠ABC﹣∠M的值不变,可以证明只有一个结论正确,请你作出正确的选择并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C,抛物线的顶点为P.
(1)如图1,连接AP,分别求出抛物线与直线AP的解析式;
(2)如图1,点D(2,3)在抛物线上,在第一象限内,直线AP上是否存在点E,使DE⊥EO?若存在,求出点E的坐标;若不存在,请说明理由.
(3)如图2,连接BC与抛物线的对称轴交于点F,在对称轴右侧的抛物线上是否存在点G,使△GPF与△GBF的面积相等?若存在,求出点G的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程与方法,探究函数y=![]() 的图象与性质.
的图象与性质.
因为y=![]() ,即y=﹣
,即y=﹣![]() +1,所以我们对比函数y=﹣
+1,所以我们对比函数y=﹣![]() 来探究.
来探究.
列表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ |
| 1 | 2 | 3 | 4 | … |
y=﹣ | … |
|
| 1 | 2 | 4 | ﹣4 | ﹣1 | 1 | ﹣ | ﹣ | … |
y= | … |
|
| 2 | 3 | 5 | ﹣3 | ﹣1 | 0 |
|
| … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以y=![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而 ;(填“增大”或“减小”)
②y=![]() 的图象是由y=﹣
的图象是由y=﹣![]() 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;
③图象关于点 中心对称.(填点的坐标)
(3)设A(x1,y1),B(x2,y2)是函数y=![]() 的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
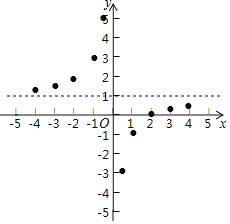
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com