
【题目】已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C,抛物线的顶点为P.
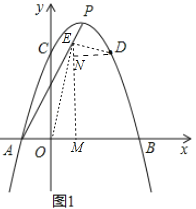
(1)如图1,连接AP,分别求出抛物线与直线AP的解析式;
(2)如图1,点D(2,3)在抛物线上,在第一象限内,直线AP上是否存在点E,使DE⊥EO?若存在,求出点E的坐标;若不存在,请说明理由.
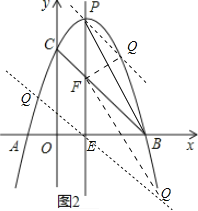
(3)如图2,连接BC与抛物线的对称轴交于点F,在对称轴右侧的抛物线上是否存在点G,使△GPF与△GBF的面积相等?若存在,求出点G的坐标;若不存在,请说明理由.

【答案】(1)抛物线的解析式为y=﹣x2+2x+3,直线AP的解析式为y=2x+2;(2)E(![]() ,
,![]() +2)或(﹣
+2)或(﹣![]() ,﹣
,﹣![]() +2);(3)点Q的坐标为(2,3),(
+2);(3)点Q的坐标为(2,3),(![]() ,﹣
,﹣![]() ).
).
【解析】(1)把A(-1,0)、![]() 两点代入y=-x+bx+c即可求出抛物线的解析式,求出点P的坐标,将点A、P两点坐标代入
两点代入y=-x+bx+c即可求出抛物线的解析式,求出点P的坐标,将点A、P两点坐标代入![]() 即可求出直线解析式;
即可求出直线解析式;
(2)设过点P与BC平行的直线与抛物线的交点为Q,根据直线BC的解析式为y=-x+3,过点P与BC平行的直线为y=-x+5,得Q的坐标为(2,3),根据PM的解析式为:![]() ,直线BC的解析式为y=-x+3,得M的坐标为(1,2),设PM与x轴交于点E,求出过点E与BC平行的直线为y=-x+1,根据
,直线BC的解析式为y=-x+3,得M的坐标为(1,2),设PM与x轴交于点E,求出过点E与BC平行的直线为y=-x+1,根据![]() ,
,
得点Q的坐标为![]() .
.
(1)由![]() 得
得![]() ,
,
则抛物线的解析式为y=﹣x2+2x+3,
∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴P(1,4),
设直线AP的解析式为y=kx+b,点A、P两点坐标代入得![]()
解得:![]() .
.
则直线AP的解析式为y=2x+2;
(2)如图1,假设AP上有一点E,使得DE⊥EO,作EM⊥OB,DN⊥EM,
则△EMO∽△DNE,
∴![]() ,
,
设E(x,y),D(2,3),
则OM=x,EM=y,EN=y﹣3,DN=2﹣x,
∴![]()
又∵y=2x+2,
解得:x=![]() ,
,
∴y=![]() +2,
+2,
∴E(![]() ,
,![]() +2)或(﹣
+2)或(﹣![]() ,﹣
,﹣![]() +2);
+2);
(3)设过点P与BC平行的直线与抛物线的交点为Q,
∵P点的坐标为(1,4),直线BC的解析式为y=﹣x+3,
∴过点P与BC平行的直线为y=﹣x+5
由![]()
得Q的坐标为(2,3),
∵PF的解析式为x=1,直线BC的解析式为y=﹣x+3,
∴F的坐标为(1,2),
设PM与x轴交于点E,
∵PF=EF=2,
∴过点E与BC平行的直线为y=﹣x+1,
由 ![]()
得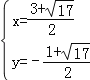 或
或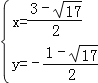 (不合题意,舍去),
(不合题意,舍去),
∴点Q的坐标为(![]() ,﹣
,﹣![]() ),
),
∴使得△QMB与△PMB的面积相等的点Q的坐标为(2,3),(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】某校准备到服装超市购一批演出服装(男,女服装价格相同)以供文艺汇演使用,一套服装定价![]() 元,领结(花)每条定价
元,领结(花)每条定价![]() 元,适逢新中国成立
元,适逢新中国成立![]() 周年,服装超市开展促销活动,向客户提供两种优惠方案:
周年,服装超市开展促销活动,向客户提供两种优惠方案:
①买一套服装送一条领结(花);
②服装和领结(花)都按定价的![]() 销售.
销售.
现该校要到该服装超市购买服装![]() 套,领结(花)
套,领结(花)![]() 条
条![]()
![]() .
.
(1)若该校按方案①购买.需付款_______ 元(用含![]() 的式子表示);若该校按方案②购买.需付款 元(用含
的式子表示);若该校按方案②购买.需付款 元(用含![]() 的式子表示);
的式子表示);
(2)若![]() ,通过计算说明此时按哪种方案付款比较合算;
,通过计算说明此时按哪种方案付款比较合算;
(3)当![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并计算出需付款多少元.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并计算出需付款多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中AD是∠A的外角平分线,P是AD上一动点且不与点A、D重合,记PB+PC=a,AB+AC=b,则a、b的大小关系是( )
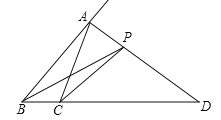
A.a>b B.a=b C.a<b D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为⊙O外一点,PA、PB分别切⊙O于A、B两点,OP交⊙O于点C,连接BO并延长交⊙O于点D,交PA的延长线于点E,连接AD、BC.下列结论:①AD∥PO;②△ADE∽△PCB;③tan∠EAD=![]() ;④BD2=2ADOP.其中一定正确的是( )
;④BD2=2ADOP.其中一定正确的是( )

A. ①③④ B. ②④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶情况记录如下(单位:千米):
+10,﹣8,+7,﹣15,+6,﹣16,+4,﹣2
(1)A处在岗亭何方?距离岗亭多远?
(2)若摩托车每行驶1千米耗油a升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
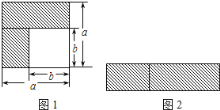
(1)如图1,可以求出阴影部分的面积是______ (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是______,长是______,面积是______.(写成多项式乘法的形式)
(3)比较左、右两图的阴影部分面积,可以得到乘法公式______.(用式子表达)
(4)运用你所得到的公式,计算下列各题:
①10.3×9.7
②(2m+n-p)(2m-n+p)
查看答案和解析>>
科目:初中数学 来源: 题型:
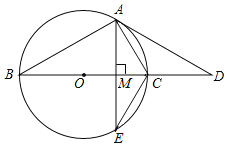
【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3x2+x+2,B=﹣3x2+9x+6.
(1)求2A﹣![]() B;
B;
(2)若2A﹣![]() B与
B与![]() 互为相反数,求C的表达式;
互为相反数,求C的表达式;
(3)在(2)的条件下,若x=2是C=2x+7a的解,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
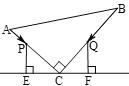
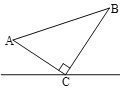
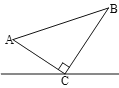
【题目】如图所示,△ABC中,∠ACB=90°,AC=6cm,BC =8cm.点P从A点出发,沿![]() 路径向终点B运动,点Q从B点出发,沿
路径向终点B运动,点Q从B点出发,沿![]() 路径向终点A运动.点P 和Q分别
路径向终点A运动.点P 和Q分别![]() 和
和![]() 的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.
的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com