
【题目】乘法公式的探究及应用.
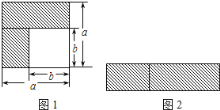
(1)如图1,可以求出阴影部分的面积是______ (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是______,长是______,面积是______.(写成多项式乘法的形式)
(3)比较左、右两图的阴影部分面积,可以得到乘法公式______.(用式子表达)
(4)运用你所得到的公式,计算下列各题:
①10.3×9.7
②(2m+n-p)(2m-n+p)
【答案】(1)a2-b2;(2)a-b;a+b; ![]() ;(3)
;(3)![]() ;(4)①99.91;②4m2-n2+2np-p2.
;(4)①99.91;②4m2-n2+2np-p2.
【解析】
(1)利用正方形的面积公式就可求出;
(2)仔细观察图形就会知道长,宽,由面积公式就可求出面积;
(3)建立等式就可得出;
(4)利用平方差公式就可方便简单的计算.
解:(1)利用正方形的面积公式可知:阴影部分的面积=a2-b2;
故答案为:a2-b2;
(2)由图可知矩形的宽是a-b,长是a+b,所以面积是(a+b)(a-b);
故答案为:a-b,a+b,(a+b)(a-b);
(3)(a+b)(a-b)=a2-b2(等式两边交换位置也可);
故答案为:(a+b)(a-b)=a2-b2;
(4)①解:原式=(10+0.3)×(10-0.3)
=102-0.32
=100-0.09
=99.91;
②解:原式=[2m+(n-p)][2m-(n-p)]
=(2m)2-(n-p)2
=4m2-n2+2np-p2.


科目:初中数学 来源: 题型:
【题目】(1)如图,点M在数轴上对应的数为-4.点N在点M右边距M点6个单位长度,求点N对应的数;

(2)在(1)的条件下.保持N点静止不动,点M沿数轴以每秒1个单位长度的速度匀速向右运动,经过多长时间M,N两点相距4个单位长度;
(3)若已知点M,N在数轴上对应的数分别为-6、2.点M以每秒3个单位长度的速度沿数轴向右运动,N以每秒2个单位长度的速度同时沿数轴向右运动,当M,N两点相距![]() 个单位长度时,请直接写出点M所对应的数.
个单位长度时,请直接写出点M所对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题:
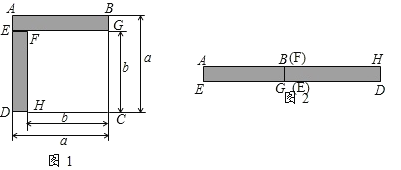
(1)如图1,已知正方形![]() 的边长为
的边长为![]() ,正方形
,正方形![]() 的边长为
的边长为![]() ,长方形
,长方形![]() 和
和![]() 为阴影部分,则阴影部分的面积是____.(写成平方差的形式)
为阴影部分,则阴影部分的面积是____.(写成平方差的形式)
(2)将图1中的长方形![]() 和
和![]() 剪下来,拼成图2所示的长方形,则长方形
剪下来,拼成图2所示的长方形,则长方形![]() 的面积是____.(写成多项式相乘的形式)
的面积是____.(写成多项式相乘的形式)
(3)比较图1与图2的阴影部分的面积,可得乘法公式____.
(4)利用所得公式计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,C点在y轴上,B点在x轴上,A点从C点出发沿正西运动,B点在x轴上运动.

(1)如图1当∠ABC=∠ABD,作∠CBO的平分线交AC的延长线于E,作CF⊥EB于F.求证:∠ABD=∠ECF;
(2)如图2,在(1)的条件下,延长AB与∠BCO的平分线交于M点,下列结论:
①∠M的度数不变;
②∠ABC﹣∠M的值不变,可以证明只有一个结论正确,请你作出正确的选择并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C,抛物线的顶点为P.
(1)如图1,连接AP,分别求出抛物线与直线AP的解析式;
(2)如图1,点D(2,3)在抛物线上,在第一象限内,直线AP上是否存在点E,使DE⊥EO?若存在,求出点E的坐标;若不存在,请说明理由.
(3)如图2,连接BC与抛物线的对称轴交于点F,在对称轴右侧的抛物线上是否存在点G,使△GPF与△GBF的面积相等?若存在,求出点G的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
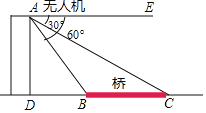
【题目】小亮在某桥附近试飞无人机,如图,为了测量无人机飞行的高度AD,小亮通过操控器指令无人机测得桥头B,C的俯角分别为∠EAB=60°,∠EAC=30°,且D,B,C在同一水平线上.已知桥BC=30米,求无人机飞行的高度AD.(精确到0.01米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程与方法,探究函数y=![]() 的图象与性质.
的图象与性质.
因为y=![]() ,即y=﹣
,即y=﹣![]() +1,所以我们对比函数y=﹣
+1,所以我们对比函数y=﹣![]() 来探究.
来探究.
列表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ |
| 1 | 2 | 3 | 4 | … |
y=﹣ | … |
|
| 1 | 2 | 4 | ﹣4 | ﹣1 | 1 | ﹣ | ﹣ | … |
y= | … |
|
| 2 | 3 | 5 | ﹣3 | ﹣1 | 0 |
|
| … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以y=![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而 ;(填“增大”或“减小”)
②y=![]() 的图象是由y=﹣
的图象是由y=﹣![]() 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;
③图象关于点 中心对称.(填点的坐标)
(3)设A(x1,y1),B(x2,y2)是函数y=![]() 的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
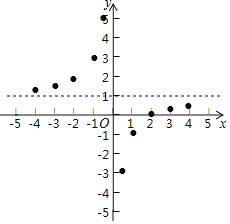
查看答案和解析>>
科目:初中数学 来源: 题型:
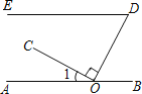
【题目】如图所示,点O在直线AB上,OC⊥OD,∠EDO与∠1互余,OF平分∠COD交DE于点F,若∠OFD=70°,求∠1的度数.
(1)使用直尺和圆规,补全图形;(保留作图痕迹).
(2)解∵∠EDO与∠1互余
∴∠EDO+∠1=90°
∵OC⊥OD
∴∠COD=90°
∴∠EDO+∠1+∠COD=180°
∴______+______=180°
∴ED∥AB.(______)
∴∠AOF=∠OFD=70°(______)
∵OF平分∠COD,(已知)
∴∠COF=![]() ∠COD=45°(______)
∠COD=45°(______)
∴∠1=∠AOF-∠COF=______°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com