
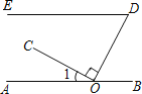
【题目】如图所示,点O在直线AB上,OC⊥OD,∠EDO与∠1互余,OF平分∠COD交DE于点F,若∠OFD=70°,求∠1的度数.
(1)使用直尺和圆规,补全图形;(保留作图痕迹).
(2)解∵∠EDO与∠1互余
∴∠EDO+∠1=90°
∵OC⊥OD
∴∠COD=90°
∴∠EDO+∠1+∠COD=180°
∴______+______=180°
∴ED∥AB.(______)
∴∠AOF=∠OFD=70°(______)
∵OF平分∠COD,(已知)
∴∠COF=![]() ∠COD=45°(______)
∠COD=45°(______)
∴∠1=∠AOF-∠COF=______°.
【答案】(1)见解析;(2)∠EDO,∠AOD,同旁内角互补,两直线平行;两直线平行,内错角相等;角平分线的定义,25
【解析】
(1)依据OF平分∠COD交DE于点F,进行作图即可;
(2)依据同旁内角互补,两直线平行,判定ED∥AB,再根据平行线的性质以及角平分线的定义,即可得到∠1的度数.
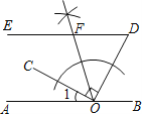
解:(1)如图所示,OF平分∠COD交DE于点F,
(2)∵∠EDO与∠1互余,
∴∠EDO+∠1=90°,
∵OC⊥OD,
∴∠COD=90°,
∴∠EDO+∠1+∠COD=180°,
∴∠EDO+∠AOD=180°,
∴ED∥AB,(同旁内角互补,两直线平行)
∴∠AOF=∠OFD=70°,(两直线平行,内错角相等)
∵OF平分∠COD,(已知)
∴∠COF=![]() ∠COD=45°,(角平分线的定义)
∠COD=45°,(角平分线的定义)
∴∠1=∠AOF-∠COF=25°.
故答案为:∠EDO,∠AOD,同旁内角互补,两直线平行;两直线平行,内错角相等;角平分线的定义,25.


科目:初中数学 来源: 题型:
【题目】某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正、减产记为负):
![]()
(1)根据记录的数据可知该厂星期四生产自行车________ 辆;
(2)根据记录的数据可知该厂本周实际生产自行车______辆;
(3)该厂实行每日计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖励15元;少生产一辆另扣20元,那么该厂工人这一周的工资总额是多少?
(4)若将上面第(3)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,在此方式下这一周工人的工资与按日计件的工资哪一个更多?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
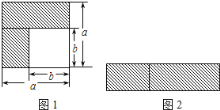
(1)如图1,可以求出阴影部分的面积是______ (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是______,长是______,面积是______.(写成多项式乘法的形式)
(3)比较左、右两图的阴影部分面积,可以得到乘法公式______.(用式子表达)
(4)运用你所得到的公式,计算下列各题:
①10.3×9.7
②(2m+n-p)(2m-n+p)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
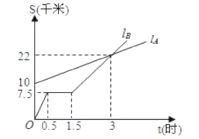
(1)B出发时与A相距___千米。
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是___小时。
(3)B出发后___小时与A相遇。
(4)若B的自行车不发生故障,保持出发时的速度前进,___小时与A相遇,相遇点离B的出发点___千米。在图中表示出这个相遇点C.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3x2+x+2,B=﹣3x2+9x+6.
(1)求2A﹣![]() B;
B;
(2)若2A﹣![]() B与
B与![]() 互为相反数,求C的表达式;
互为相反数,求C的表达式;
(3)在(2)的条件下,若x=2是C=2x+7a的解,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题时,我们一般先仔细读题干,找出有用信息作为已知条件,然后用这些信息解决问题,但是有的题目信息比较明显,我们把这样的信息称为显性条件,而有的信息不太明显需要结合图形,特殊式子成立的条件,实际问题等发现隐含信息作为条件,这样的条件称为隐含条件,所以我们在做题时更注意发现题目中的隐含条件
(阅读理解)
读下面的解题过程,体会加何发现隐含条件,并回答.
化简:![]() .解:隐含条件1-3x≥0,解得:x
.解:隐含条件1-3x≥0,解得:x![]() ,∴原式=(1-3x)-(1-x)=1-3x-1+x=-2x
,∴原式=(1-3x)-(1-x)=1-3x-1+x=-2x
(启发应用)
已知△ABC三条边的长度分别是![]() ,记△ABC的周长为C△ABC
,记△ABC的周长为C△ABC
(1)当x=2时,△ABC的最长边的长度是______(请直接写出答案).
(2)请求出C△ABC(用含x的代数式表示,结果要求化简).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在“元旦”期间对顾客实行优惠,规定一次性购物优惠办法:
少于200元,不予优惠;高于200元但低于500元时,九折优惠;消费500元或超过500元时,其中500元部分给予九折优惠,超过500元部分给予八折优惠.根据优惠条件完成下列任务:
(1)王老师一次性购物600元,他实际付款多少元?
(2)若顾客在该超市一次性购物x元,当x小于500但不小于200时,他实际付款0.9x,当x大于或等于500元时,他实际付款多少元?(用含x的代数式表示)
(3)如果王老师两次购物货款合计820元,第一次购物的货款为a元(200<a<300),用含a的式子表示王老师两次购物实际付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的对称中心为坐标原点O,AD⊥y轴于点E(点A在点D的左侧),经过E、D两点的函数y=﹣![]() x2+mx+1(x≥0)的图象记为G1,函数y=﹣
x2+mx+1(x≥0)的图象记为G1,函数y=﹣![]() x2﹣mx﹣1(x<0)的图象记为G2,其中m是常数,图象G1、G2合起来得到的图象记为G.设矩形ABCD的周长为L.
x2﹣mx﹣1(x<0)的图象记为G2,其中m是常数,图象G1、G2合起来得到的图象记为G.设矩形ABCD的周长为L.
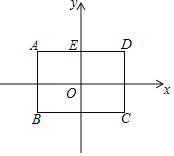
(1)当点A的横坐标为﹣1时,求m的值;
(2)求L与m之间的函数关系式;
(3)当G2与矩形ABCD恰好有两个公共点时,求L的值;
(4)设G在﹣4≤x≤2上最高点的纵坐标为y0,当![]() ≤y0≤9时,直接写出L的取值范围.
≤y0≤9时,直接写出L的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com