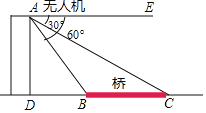
[题目]小亮在某桥附近试飞无人机.如图.为了测量无人机飞行的高度AD.小亮通过操控器指令无人机测得桥头B.C的俯角分别为∠EAB=60°.∠EAC=30°.且D.B.C在同一水平线上．已知桥BC=30米.求无人机飞行的高度AD．(精确到0.01米．参考数据:≈1.414.≈1.732) 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】小亮在某桥附近试飞无人机，如图，为了测量无人机飞行的高度AD，小亮通过操控器指令无人机测得桥头B，C的俯角分别为∠EAB=60°，∠EAC=30°，且D，B，C在同一水平线上．已知桥BC=30米，求无人机飞行的高度AD．（精确到0.01米．参考数据：≈1.414，≈1.732）

【答案】25.98米.

【解析】由∠EAB=60°、∠EAC=30°可得出∠CAD=60°、∠BAD=30°，进而可得出CD=AD、BD=AD，再结合BC=30即可求出AD的长度．

∵∠EAB=60°，∠EAC=30°，

∴∠CAD=60°，∠BAD=30°，

∴CD=ADtan∠CAD=AD，BD=ADtan∠BAD=AD，

∴BC=CD﹣BD=AD=30，

∴AD=15≈25.98，

答：无人机飞行的高度AD为25.98米．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

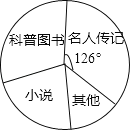
【题目】2018年东营市教育局在全市中小学开展了“情系疏勒书香援疆”捐书活动，200多所学校的师生踊跃参与，向新疆疏勒县中小学共捐赠爱心图书28.5万余本．某学校学生社团对本校九年级学生所捐图书进行统计，根据收集的数据绘制了下面不完整的统计图表．请你根据统计图表中所提供的信息解答下列问题：

图书种类	频数（本）	频率
名人传记	175	a
科普图书	b	0.30
小说	110	c
其他	65	d

（1）求该校九年级共捐书多少本；

（2）统计表中的a=　　，b=　　，c=　　，d=　　；

（3）若该校共捐书1500本，请估计“科普图书”和“小说”一共多少本；

（4）该社团3名成员各捐书1本，分别是1本“名人传记”，1本“科普图书”，1本“小说”，要从这3人中任选2人为受赠者写一份自己所捐图书的简介，请用列表法或树状图求选出的2人恰好1人捐“名人传记”，1人捐“科普图书”的概率．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，点P是△ABC的外角∠EAB的平分线AF上的一点，PD垂直平分BC，PGAB，求证：BG=AG+AC．

查看答案和解析>>

科目：初中数学 来源： 题型：

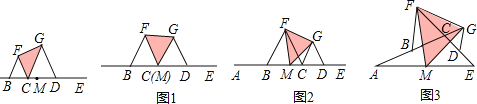
【题目】在图1至图3中，点B是线段AC的中点，点D是CE的中点，△BCF和△CDG都是等边三角形，点M为AE的中点，连接FG．

（1）如图1，若点E在AC的延长线上，点M与点C重合，则△FMG　　　　　　等边三角形（填“是”或“不是”）

（2）将图1中的CE缩短，得到图2．求证：△FMG为等边三角形；

（3）将图2中的CE绕点E顺时针旋转一个锐角，得到图3．求证：△FMG为等边三角形．

查看答案和解析>>

科目：初中数学 来源： 题型：

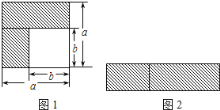
【题目】乘法公式的探究及应用．

（1）如图1，可以求出阴影部分的面积是______　（写成两数平方差的形式）；

（2）如图2，若将阴影部分裁剪下来，重新拼成一个长方形，它的宽是______，长是______，面积是______．（写成多项式乘法的形式）

（3）比较左、右两图的阴影部分面积，可以得到乘法公式______．（用式子表达）

（4）运用你所得到的公式，计算下列各题：

①10.3×9.7

②（2m+n-p）（2m-n+p）

查看答案和解析>>

科目：初中数学 来源： 题型：

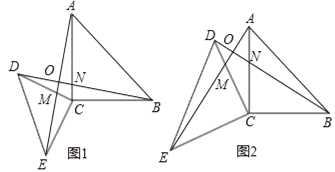
【题目】已知：△ACB和△DCE都是等腰直角三角形，∠ACB=∠DCE=90°，连接AE，BD交于点O，AE与DC交于点M，BD与AC交于点N．

(1)如图1，猜想AE与BD的数量关系与位置关系，并加以证明.

(2)如图2，若AC=DC，在不添加任何辅助线的情况下，请直接写出图2中四对全等的直角三角形．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图,,分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.

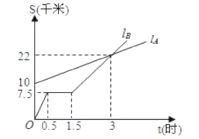
(1)B出发时与A相距___千米。

(2)走了一段路后，自行车发生故障，进行修理，所用的时间是___小时。

(3)B出发后___小时与A相遇。

(4)若B的自行车不发生故障，保持出发时的速度前进，___小时与A相遇，相遇点离B的出发点___千米。在图中表示出这个相遇点C.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在解决数学问题时，我们一般先仔细读题干，找出有用信息作为已知条件，然后用这些信息解决问题，但是有的题目信息比较明显，我们把这样的信息称为显性条件，而有的信息不太明显需要结合图形，特殊式子成立的条件，实际问题等发现隐含信息作为条件，这样的条件称为隐含条件，所以我们在做题时更注意发现题目中的隐含条件

（阅读理解）

读下面的解题过程，体会加何发现隐含条件，并回答．

化简：．解：隐含条件1-3x≥0，解得：x，∴原式=（1-3x）-（1-x）=1-3x-1+x=-2x