
【题目】已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连接AE,BD交于点O,AE与DC交于点M,BD与AC交于点N.
(1)如图1,猜想AE与BD的数量关系与位置关系,并加以证明.
(2)如图2,若AC=DC,在不添加任何辅助线的情况下,请直接写出图2中四对全等的直角三角形.
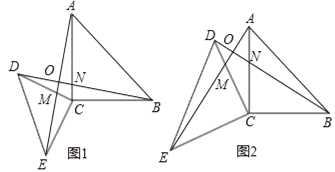
【答案】(1)AE=BD,AE⊥BD;(2)△ACB≌△DCE;△EMC≌△BNC;△AON≌△DOM;△AOB≌△DOE
【解析】
(1)根据全等三角形的性质即可求证△ACE≌△BCD,从而可知AE=BD、AE⊥BD;
(2)根据条件即可判断图中的全等直角三角形;
解:(1)AE=BD,AE⊥BD.
理由如下:
∵△ACB和△DCE都是等腰直角三角形,
∠ACB=∠DCE=90°,
∴AC=BC,DC=EC,
∴∠ACB+∠ACD=∠DCE+∠ACD,
∴∠BCD=∠ACE
在△ACE与△BCD中,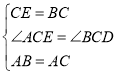
∴△ACE≌△BCD(SAS)
∴AE=BD,∠BDC=∠AEC
又∵在△DOM与△CME中,∠DMA=∠CME
∴∠DOM=∠MCE=90°
∴AE⊥BD
(2) ∵AC=DC,
∴AC=CD=EC=CB,∠ACB=∠DCE
△ACB≌△DCE(SAS);
由(1)可知:∠AEC=∠BDC,∠EAC=∠DBC
∴∠DOM=90°,
∵∠AEC=∠CAE=∠CBD,
∴△EMC≌△BNC(ASA),
∴CM=CN,
∴DM=AN,
△AON≌△DOM(AAS),
∵DE=AB,AO=DO,
∴△AOB≌△DOE(HL)


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .
.

(1)若BC=7,BD=4,则点![]() 到
到![]() 的距离是________;
的距离是________;
(2)若![]() ,点
,点![]() 到
到![]() 的距离是8,则
的距离是8,则![]() 的长是________.
的长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
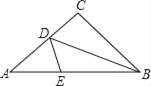
【题目】如图,三角形纸牌中,AB=8cm,BC=6cm,AC=5cm,沿着过△ABC的顶点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△AED周长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D、E在同一条直线上,已知AB = FC,AD = FE, BC=DE.
(1)求证:△ABD≌△FCE.
(2)AB与FC的位置关系是_________(请直接写出结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
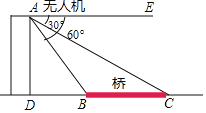
【题目】小亮在某桥附近试飞无人机,如图,为了测量无人机飞行的高度AD,小亮通过操控器指令无人机测得桥头B,C的俯角分别为∠EAB=60°,∠EAC=30°,且D,B,C在同一水平线上.已知桥BC=30米,求无人机飞行的高度AD.(精确到0.01米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD>AB,点P是CD边上的任意一点(不含C,D两端点),过点P作PF∥BC,交对角线BD于点F.
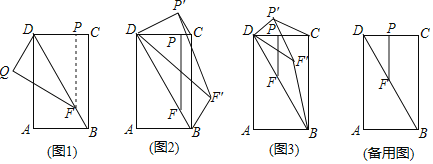
(1)如图1,将△PDF沿对角线BD翻折得到△QDF,QF交AD于点E.求证:△DEF是等腰三角形;
(2)如图2,将△PDF绕点D逆时针方向旋转得到△P'DF',连接P'C,F'B.设旋转角为α(0°<α<180°).
①若0°<α<∠BDC,即DF'在∠BDC的内部时,求证:△DP'C∽△DF'B.
②如图3,若点P是CD的中点,△DF'B能否为直角三角形?如果能,试求出此时tan∠DBF'的值,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某种蜡烛在燃烧过程中高度与时间之间关系的图像,由图像解答下列问题:
(1)此蜡烛燃烧1小时后,高度为 cm;经过 小时燃烧完毕;
(2)求这个蜡烛在燃烧过程中高度与时间之间关系的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 到点
到点![]() 、点
、点![]() 的距离相等,动点
的距离相等,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴向右匀速运动,设运动时间为
个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() (
(![]() 大于
大于![]() 秒.
秒.
![]()
(1)点![]() 表示的数是______.
表示的数是______.
(2)求当![]() 等于多少秒时,点
等于多少秒时,点![]() 到达点
到达点![]() 处?
处?
(3)点![]() 表示的数是______(用含字母
表示的数是______(用含字母![]() 的式子表示)
的式子表示)
(4)求当![]() 等于多少秒时,
等于多少秒时,![]() 、
、![]() 之间的距离为
之间的距离为![]() 个单位长度.
个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A=2x2+ax﹣5y+b,B=bx2﹣![]() x﹣
x﹣![]() y﹣3.
y﹣3.
(1)求3A﹣(4A﹣2B)的值;
(2)当x取任意数值,A﹣2B的值是一个定值时,求(a+![]() A)﹣(2b+
A)﹣(2b+![]() B)的值.
B)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com